Chapter 6 - Recursion

In this assignment you are to use ArrayList of ArrayLists and Recursion. Although you are solving the hailstone problem, you are being asked to report the longest hailstone sequence for all sequences from 1 to n where n is input by the user.

The hailstone sequence is an algorithm that starts with a positive integer and then, through a series of changes ends up with (hopefully) a never-ending sequence of 4-2-1.
For any n > 1,

If n is even, divide it by two and repeat
If the number is odd, multiply by three and add one, then repeat
Hailstone Class
Your Java solution to hailstone will be a separate class. The class should contain an ArrayList to store the values generated. The constructor will receive a positive long integer (along with the ArrayList) and will verify that the integer is greater than zero (changing it to a 1 if it is not) , then call a recursive method that creates and stores in the ArrayList the hailstone sequence until the number 1 is reached.

The ArrayList parameter will have a record of the complete sequence of numbers generated. For example, if called with 5 the list would contain [ 5, 16, 8, 4, 2, 1].

Driver
Your driver program will save each such sequence in an ArrayList (so you will have an ArrayList of ArrayLists) after looping through the numbers specified by the user.

The Driver will begin by asking the user to enter a positive integer. (This is just an integer, we are using long integers above because we don’t know how big they might get.) It will then enter a counting loop from 1 to the number entered. For each "i", it will create a HailStone object, passing it both "i" and an ArrayList to store the values.
Since hailStone has a separate method to do the actual calculationsr, you can call it from the HailStone constructor or your Driver (your choice).
At the end of your counting loop, you will have a an arrayList of arrayLists. Determine which of the sequences is longest. Note this is done after all the data is stored, not while the data set is being created.

Output
Provide explanatory output such as this:
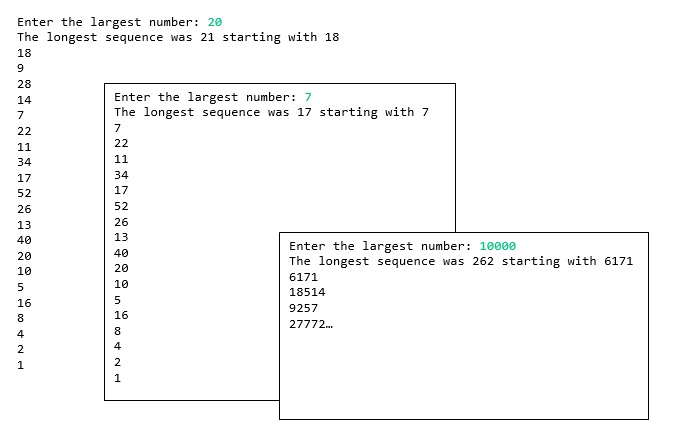To generate this output, you MUST use a a recursive display method to repeatedly delete the first element in the sequence and show it on the console, until the list is empty. dd The latter is pretty simple and may be implemented as a static function that is called from main().