Chapter 13: Graphs
Data Structures and Algorithms in Java
CpSc 374
Introduction to Graphs
- Trees are a specialized form of a graph
- There is no equivalent of the root
- No distinguished node
- Nodes are called vertices.
- These entities may model many things
- May contain large records of information (or a reference)
- Links are called edges:
- MayIndicate relationships between vertices
- be directed or undirected
- be weighted or unweighted
Some Additional Terms
- Vertex A is a neighbor of vertex D if
- There exists a single edge connecting D to A
- We also say that A is adjacent to D
- A path is a sequence of edges between vertices
- May be multiple paths from C to D
- A path may end at its starting point
- A graph is connected if there is at least one path from every vertex to every other vertex
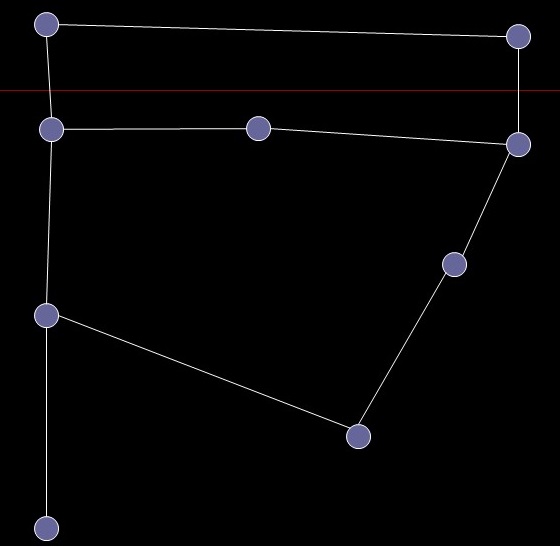
- Undirected, unweighted connected graph
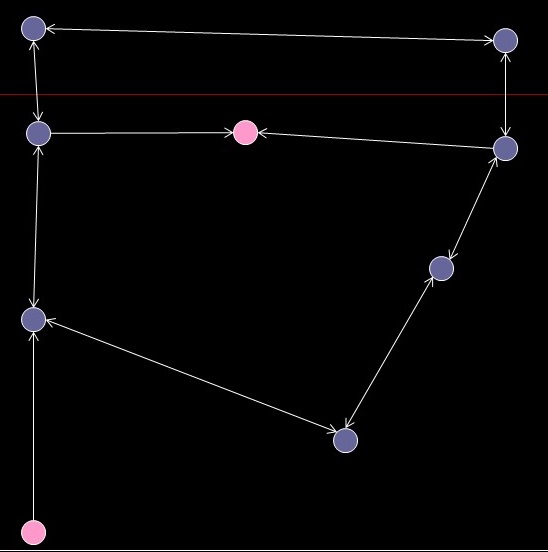
- Directed, unweighted, non-connected graph
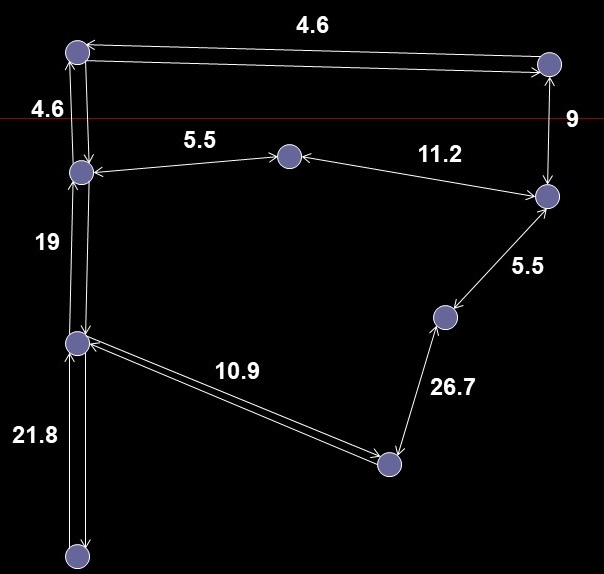
- Directed, weighted, connected graph
Representing Graphs
- A single node may have 0 or more exiting edges
- A single node may have 0 or more incoming edges
- Previously we always had a limit on the number of exiting edges
- A B-tree of order M could have M exiting edges - references to other nodes
- Normally not concerned with how many incoming edges there are - how many references there are to this node
- Representing a Vertex
class Vertex
{
public char label; // label (e.g. 'A')
public boolean wasVisited;
public Vertex(char lab) // constructor
{
label = lab;
wasVisited = false;
}
} // end class Vertex
Representing Edges using an
Adjacency List
- An array (or list) of lists
- Each vertex is an item in the array
- The (possibly ordered) list contains all neighbors
- Usually, node name is implicit
- 0 --> 'A' or just "node 0"

public class Node
{
public String name;
public List connections;
}
public class Edge
{
public Node start;
public Node end;
public double weight;
private directionEnum direction;
}
public class Graph
{
List nodes;
}
- Advantages
- any number of nodes
- any number of edges
- Good for a "sparse" graph
Representing Edges using Adjacency Matrix
- NxN array of ints
- Each vertex is both a row and a col in array
- Value of entry is:
- 1 if there is an edge
- 0 if there is no edge
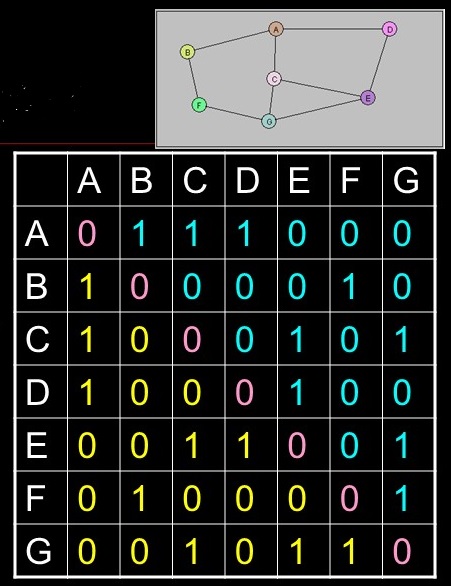
class Graph
{
private final int MAX_VERTS = 20;
private Vertex vertexList[]; // list of vertices
private int adjMat[][]; // adjacency matrix
private int nVerts; // current number of vertices
private StackX theStack;
// ------------------------------------------------------------
public Graph() // constructor
{
vertexList = new Vertex[MAX_VERTS];
// adjacency matrix
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;
for(int y=0; y<MAX_VERTS; y++) // set adjacency
for(int x=0; x<MAX_VERTS; x++) // matrix to 0
adjMat[x][y] = 0;
theStack = new StackX();
} // end constructor
// ------------------------------------------------------------
public void addVertex(char lab)
{
vertexList[nVerts++] = new Vertex(lab);
}
// ------------------------------------------------------------
public void addEdge(int start, int end)
{
adjMat[start][end] = 1;
adjMat[end][start] = 1;
}
Searches (i.e., traversals)
- How can you "visit" each node once ?
- For example - print each node (label)
- Allowed to "revisit" a node as long as you know you've already been there (and don't print it again)
- Where do you start? There is no First, no Root
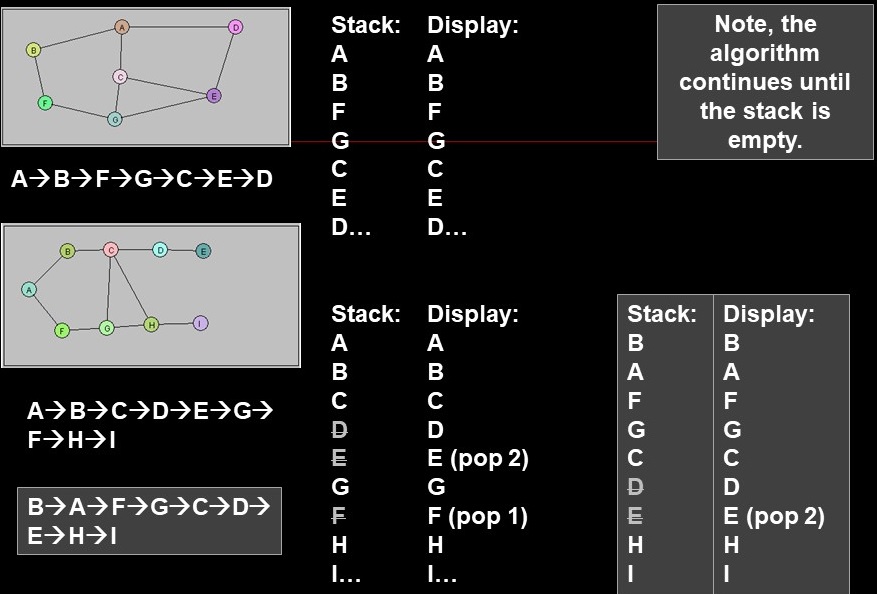
Visiting Vertices using Depth First Search (DFS)
-
Depth-First: use a Stack
- Start at any vertex
- Visit the vertex
- Mark it as visited
- Push(thisVertex)
- Select a neighbor and visit it
- If there are no neighbors,
- visit(pop(aVertex))
- If stack.isEmpty(), done!

- DFS code
- Example
Visiting Vertices using Breadth First Search (BFS)
- Breadth-First: use a Queue
- Start at any vertex
- Visit the vertex
- Mark it as visited
- For each neighbor
- a) Mark it as visited
- b) Insert(neighbor)
- While !emptyQ()
- Visit(removeQ())
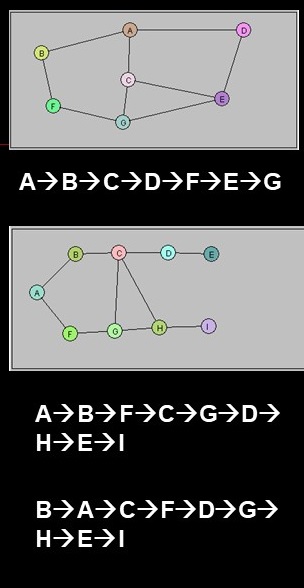
- BFS code
- Example

Minimum Spanning trees (MST)
- A subgraph, that is a tree
- Has a root (pick a start vertex)
- Connects all vertices with fewest number of edges
- E = V -1
- Can use DFS or BFS as basis...
MST using DFS
- Connects all the vertices together,
- no cycles
- with the minimum possible total edge weight
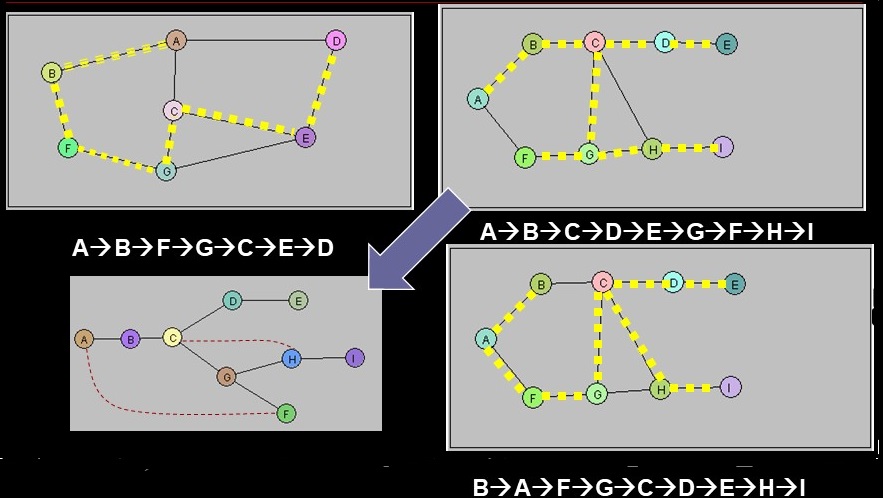
Visualization
Directed Graphs
- Edges have a direction that must be followed
- A may be connected to B, but B is not (directly) connected to A
- B is adjacent to A
- A is not adjacent to B
- If there is an edge from C to G and an edge from G to C, they are adjacent to one another
Representing Edges Adjacency Matrix
- NxN array of ints
- Each (starting) vertex is a row in array
- Value of entry is:
- 1 if there is an edge
- 0 if there is no edge
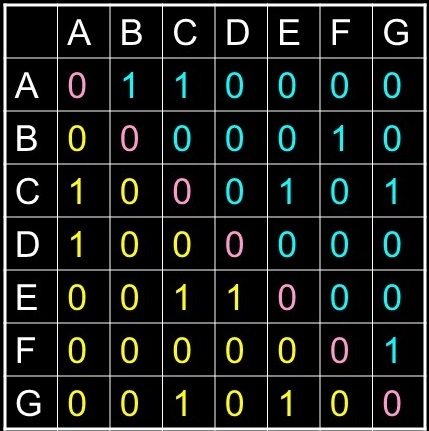
- Note: the values are Not mirrored about the diagonal
- A is connected B and C, but not to D
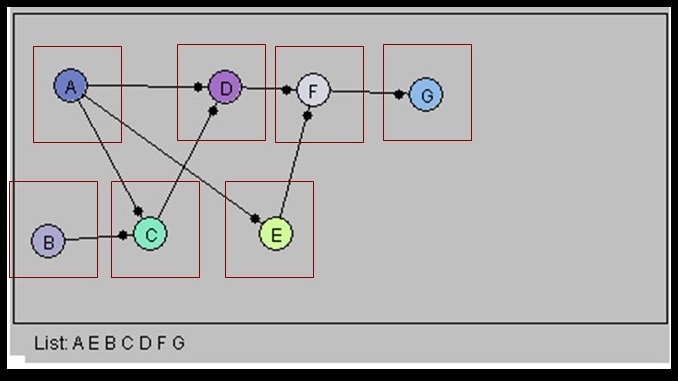
Topological Sorts in Directed Graphs
- Assuming no cycles...
- There is no path from A to A for any vertex
- While there is a vertex in the graph
- Find any vertex with no successors
- Can do this one "last"
- Insert vertex into list
- Delete vertex from graph
- The list provides a topological sort
- Multiple Cycles

- One Topological Sort
Gravity
Research
















