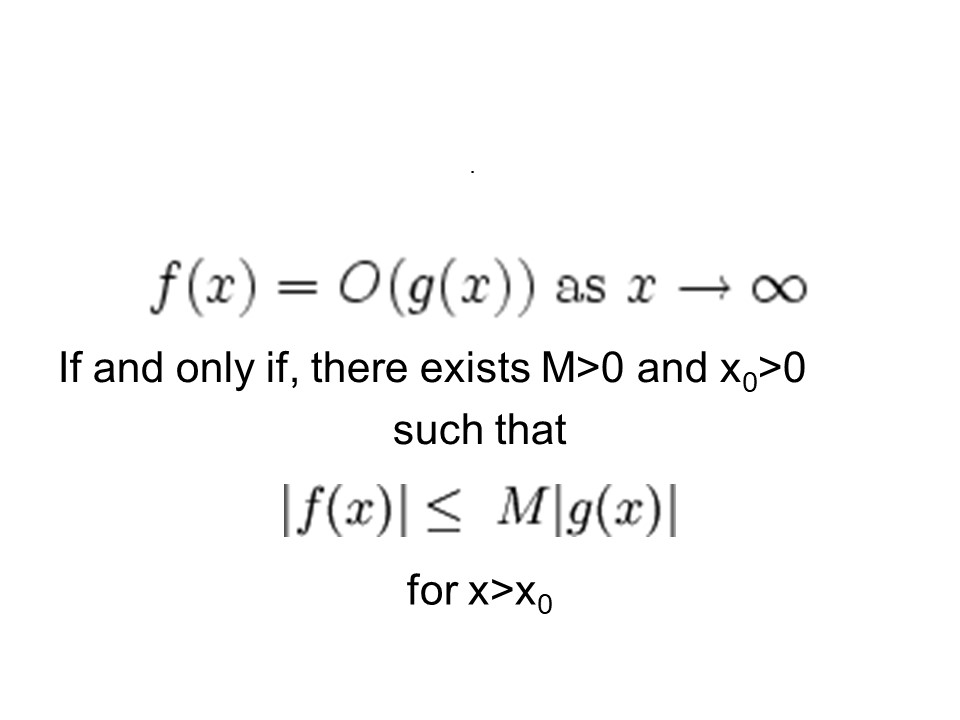Arrays

• Exist in almost every general-purpose programming language
  Google "languages without arrays" Scheme & Prolog??? out of thousands??
• Array Implementation
  • Contiguous blocks of memory for homogeneous array (most languages, but not JS)
  • Multidimensional
    row-major or column-major order
    array of arrays
  • As a data structure
    usually want no empty cells (v. sparse arrays)
• The Array Workshop Applet
  • Author's somewhat clunky visualization tool used throughout the book
  • While hard to use, the interface is consistent
    Appletviewer is no longer supported in Firefox or Chrome. Try Internet Explorer with Java enabled. Good Luck! Requires security setting changes.
  • Make sure you complete all the steps for one "command" before issuing another
  • Can usually find better on WWW
• Array Operations
  • Maintain contiguous data set
  • Insert - place item at end of array
  • Search - start at beginning and test each value
    What if not found?
    Dups --> to end of values
  • Issue - how to deal with duplicates
    In DB, keys are normally unique identifiers
  • Delete - "search" for item
    Move all "higher" items down in the array to fill vacancy
    Duplicates --> Keep looking
  • Read Logarithms & Big O Notation. Intro to time efficiency

Java Specifics

• Arrays (not vectors) are static objects
  Can't change the size - though you could implement an algorithm to do so
• In Java, name of array is a reference
• In C++, name of array is a pointer
• Java Code

  int[] ia = {0, 2, 4, 6, 8, 10};
  int[] ia = new int[numElems];
  for(int i=0; i<ia.length; i++)  
  	ia[i] = i*2;
  
  

• lab1.java
• Person.java
• See author's code that performs array insertion, search, and deletion
• Dividing a Program into Classes
  • Use a container class for the array
  • Encapsulate (protect) the data
  • Provide a way to set and get elements
  • Author's lowArray simply redefines [ ] operator (Yuk!)
  • See Chapter2's textbook code available in my folder on D2L
• Class Interfaces ... Polymorphism
  • The way other modules access the data
    Method signatures w/o implementation
  • Want "data abstraction"
  • highArray provides:
    Array data struct that know it's length (and max)
    Initialization, find, insert, delete, display
    Still need...
    Protection from overflow, sort, ...
  • See author's code with separate methods
  • Advantage to other programmers/users

Ordered Arrays

• Ordered array stores values in key sequence
• Insert - find location and move all others items "up"
• Delete - find location and move all others "down"
• Search - linear, as before, or...
  Binary search - repeatedly divide search space in half.
  Can be used for insert and delete also
• Duplicates values/keys
  Delete: keep track of number of spaces to move
  Insert and Search?
• ordered array code

Implementation of an API (Application Programming Interface)

Algorithm Analysis

• Analyze the code to determine it's "cost"
• how many computer/hardware operatiions needed?
• Run-time cost
• Fun with Math!!

Time Required for array operations?

• Unordered arrays with duplicates
  Insert - constant time
  Find - num elements
  Delete - num elements
• Unordered without duplicates
  Find - best/avg/worst
  Delete - find + ??
  Insert - find + constant
• Ordered without duplicates
  Find - best/avg/worst
  Insert - find + ??
  Delete - find + ??
• Ordered with duplicates?
  More complicated

Logarithms

• Recall 2⁵ is 32
• log₂(32) is 5
• See tables 2.3 and 2.4 on pages 62 and 63 of your text
• Ordered arrays (binary search) is fast
• Halving the search space with each test:
  Search a billion records with 30 tests!

• logb(x) =	log10(x)
  	log10(b)

• If x = b^y, then y = log_b(x) or
• If range = 2^steps, then steps = log₂(range)
• 2¹⁰ = 1,024 (1K)
• 2²⁰ is approximately 10⁶ (1M)
• 2³⁰ is approximately 10⁹1G)
• 2⁴⁰ is approximately 10¹²(1T)

Big O notation

• Used to state/compare efficiency of various algorithms (by counting "operations")
• Constant time: O(1)
  • T = 1, T = 6000, T = K (where K is some constant)
  • Insertion in an unordered Array: Constant
    Time T is some constant K, thus T = K
• Linear time: O(N)
  • T = CN + K
  • Linear Search of an array: Proportional to N
    T = K * N/2
    Lump the 1/2 into K and T = K * N (different value for K)
• Logarithmic time: O(log N) (where N is number of elems)
  • T = C log(N) + K (where C and K are some constants)
  • Binary Search: Proportional to log (N)
    T = K * log₂(N)
    Since any logarithm is related to another by a constant
    (3.322 to go from base 2 to base 10), lump the constant into K :
    T = K * log(N)
• Polynomial time: O(N²), O(N³),...
  T = C₁N² + C₂N + K

The Good, Bad and Ugly of O( )

Constant O(1) Log O(log N) Linear O(N) Polynomial Quadratic O(N2) Cubic O(N3),... Exponential O(CN)

Constants and Small N

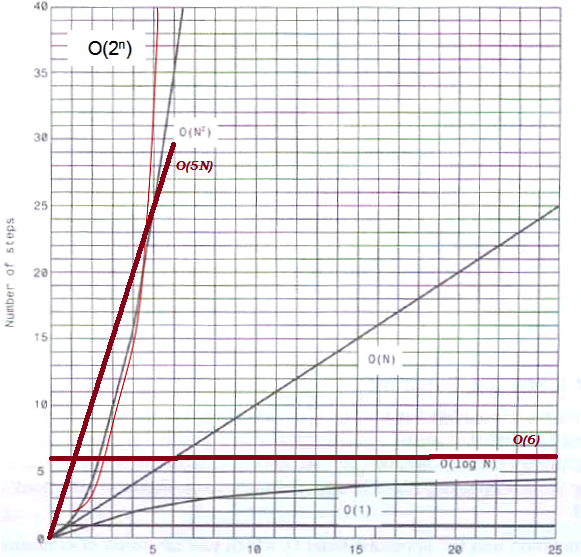
Note that O(5N) is worse than O(N2) for 0 < N < 5 Even O(6) is worse than O(N2) for 0 < N < 3 But that's not the "big picture"

Asymptotic Behavior and Large n

• Find a function g(x) that acts as an upper bound for f(x) when we ignore constants and start with a big enough size for N and care about large N
• 
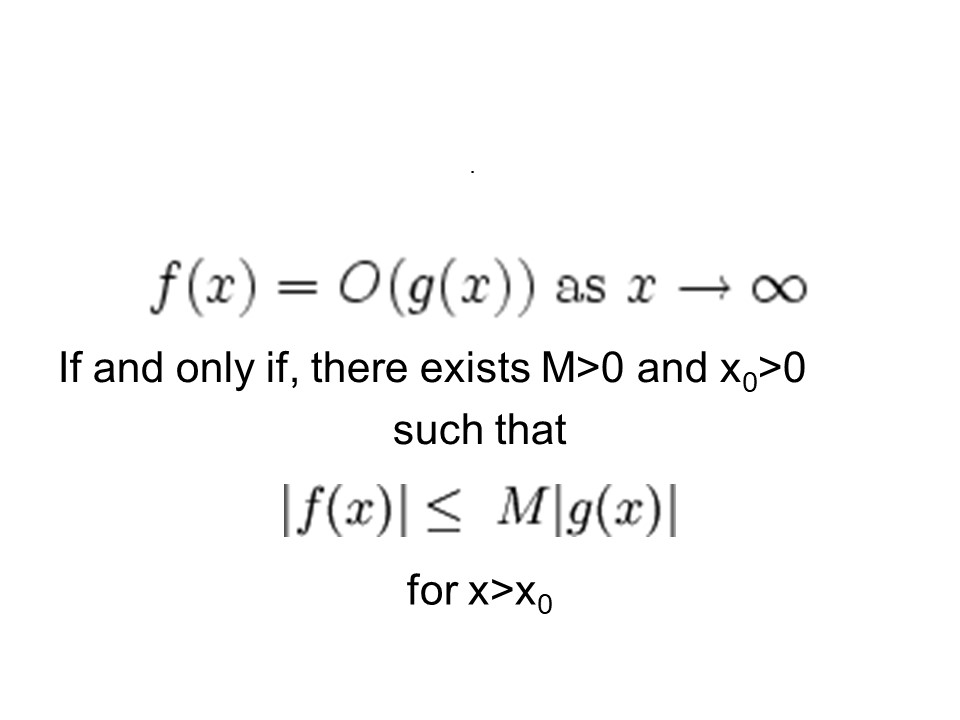
• Here's a detailed analysis of a selection sort
• Let's try it! find a java algorithm for KMP (pattern matching) and determine it's run time
  KMP at geeksfor geeks.org
  or in text here

Wrap Up

• Why Not Use Arrays for Everything
  • Other data structs are more efficient for certain (common) operations
  • Potential of overflow is always a problem
  • Doesn't always model the problem well
• Storing Objects
  • Normally, data stored/retrieved is a record or an object with various fields (members)
  • One (or more fields) represent the key
  • Search uses an equals() method, to avoid comparing references
  • Insert requires a new operation
  • Copy operations may be expensive (usually just a reference in Java)