Chapter 4: Stacks and Queues
Data Structures and Algorithms in Java
CpSc 374
A Different Kind of Structure
We looked at sorts because
- People like sorted data (by name, grade, zip code)
- Fast look up: Order of FIND for (un)ordered array?
Stacks and Queues are ordered data structs used primarily used as programming tools
-
Restricted access to data
-
Underlying data structure hidden
-
Abstract Data Type (ADT)
-
Implementation may change, perhaps to improve efficiency
Stack
- New data is always added "on top" of stack
-
The only accessible item is that which is currently on top
-
LIFO: Last-In-First-Out
-
Cheating?
- When used as an organizational tool, we sometimes access other elements directly
- If so, not really a stack
Stack Interface
- Create or Construct a stack - Allow "user" to specify max size
-
void push(item) -- insert or add an item
-
item pop() -- delete or remove an item
-
boolean isEmpty()
-
boolean isFull()
-
item peek() -- same as pop followed by push
-
int size() -- current number on stack
-
int maxSize() -- how many can I put on it
-
void grow() -- become a larger structure
To avoid a "broken" data structure, we must check first also
Pre-Conditions / Errors
Alternative
Design (using an array)
-
What are the data members (fields) of the ADT?
-
Where is the "top" of the stack?
-
What if we organized the stack in the opposite direction?
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 8 |
3 |
10 |
5 |
11 |
12 |
7 |
9 |
1 |
4 |
2 |
6 |
- Stack Code Page 120
- Critical validation not done in push
if (isFull()) {
system.out.println("Attempt to push onto a full stack: " + j);
// exit? throw exception?
}
stackArray[++top] = j;
Or
if (!isFull())
stackArray[++top] = j;
- Use Stack to reverse an array
Reverse Code
- Use Stack for matching brackets
Brackets Code
- Java has a Stack class in java.util
- java.util.AbstractCollection
- java.util.AbstractList
- java.util.Vector
- java.util.Stack
-
See docs.oracle.com
- Using Java's Stack
Stack lifo = new Stack();
for (int i = 1; i <= 10; i++)
lifo.push ( new Integer(i) );
while ( !lifo.empty() ) {
System.out.print ( lifo.pop() );
System.out.print ( ',' );
}
System.out.println (" LIFT-OFF!");
Queues - basically just a line
- Another ordered data structure
-
First-In-First-Out
-
Stack is LIFO
-
Examples of programmer uses
- Print queue
- Window's event queue
-
No "cuts" - cheating
-
Create or Construct a queue
-
Allow "user" to specify max size
- void insert(item) -- insert or add an item
- item remove() -- delete or remove an item
- item peekFront() -- get value w/o removing it
- boolean isEmpty()
- boolean isFull()
- item peekRear() -- get value w/o change
- int size() -- current number on stack
- int maxSize() -- how many can I put on it
- void grow() -- become a larger structure
Pre-Conditions / Errors
-
insert - queue must not be full
-
remove - queue must not be empty
-
peekFront - queue must not be empty
-
To avoid runtime error, queue user must check first using isEmpty() and isFull()
- Alternative?
- Minimally, you must avoid corrupting the queue
- One Design: Like a stack
- Stationary front
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 8 |
3 |
|
|
|
|
|
|
|
|
|
|
- Stationary rear
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| |
|
|
|
|
|
|
|
|
|
8 |
3 |
- Both front and rear move
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| |
|
|
|
8 |
3 |
|
|
|
|
|
|
-

-
-
-

- Special cases
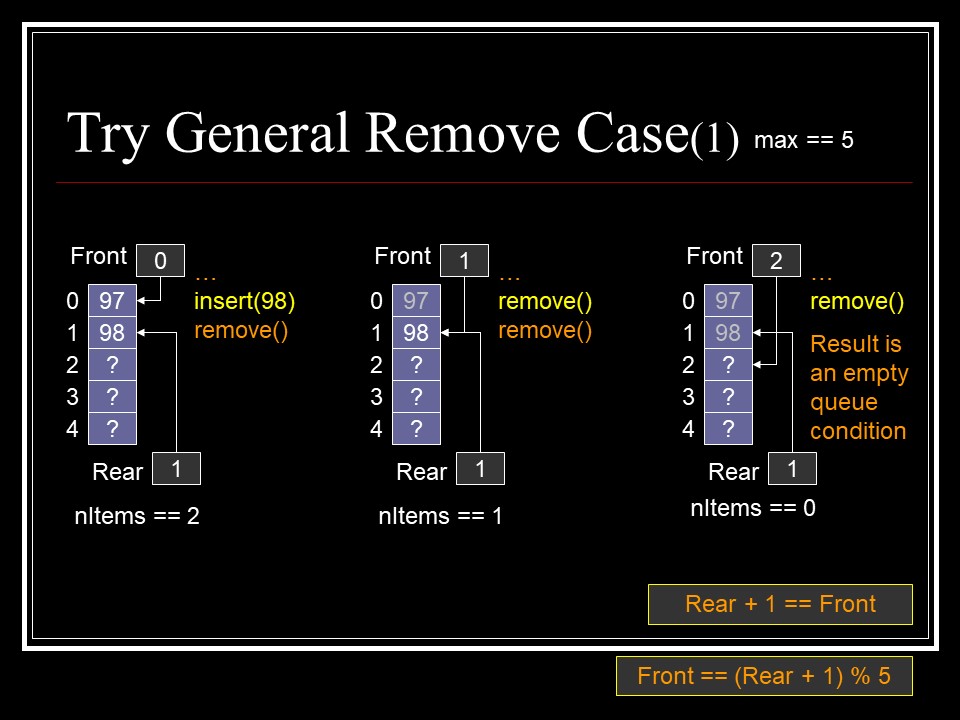
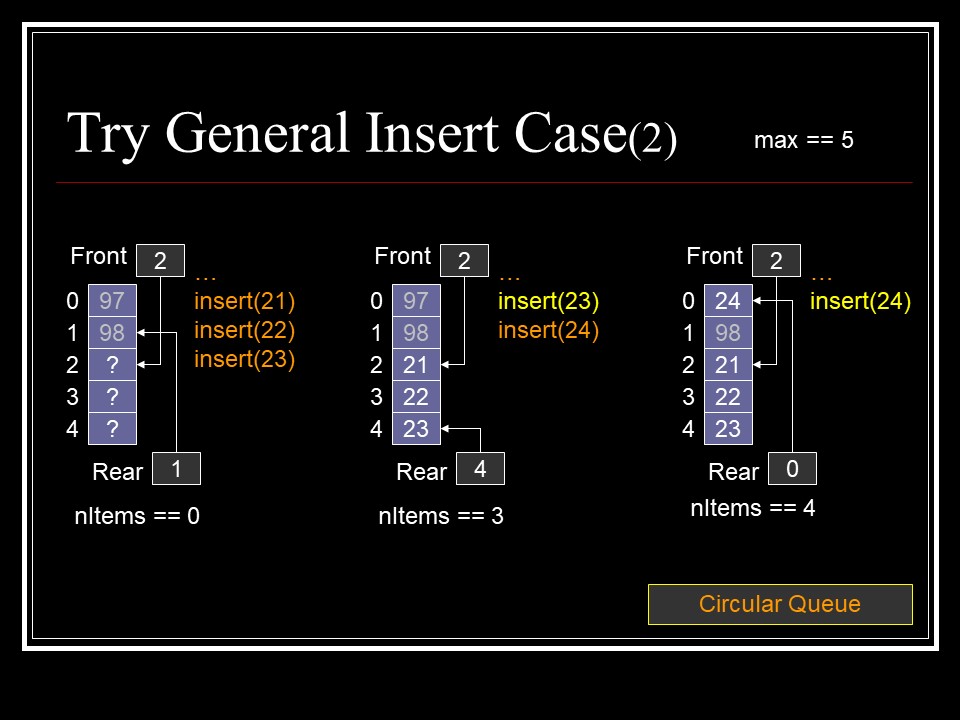
- Wrap around for insert & remove
- Empty queue
- front == (rear + 1) mod max
- nItems == 0
- Full queue
- front == (rear + 1) mod max
- nItems == max
- Initial conditions (construction) ??
Queue Implementation
- Each type needs
- public Queue (int s) {
- void insert (item) {
- long remove () {
- long peekFront() {
- boolean isEmpty() {
- boolean isFull() {
- int size() {
-
Queue Code
- Java has a queue data structure.
See
docs.oracle.com
- Is an array the best implementation for a queue?
- Implementation of double-ended queue needs:
- addFirst(item e) // and addLast(item e)
- Item e getLast() // and getFirst()
-
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 8 |
3 |
10 |
5 |
11 |
12 |
7 |
9 |
1 |
4 |
2 |
6 |
Front: 3
Rear: 8
- Most ArrayDeque operations run in amortized constant time.
- Amortization applies to our grow() method
- Some ops are O(N) - check description
Priority Queues - permits "cutting" in the line
- Items are ordered by priority, not when they arrive, i.e., not FIFO
- That means we can't use earlier code!
- Could have classes of data ordered by priority
- Within each class, still ordered by arrival
- Restaurant with
- Reservations
- Priority seating (call ahead)
- Walk-ins
- Computer Interrupts
- CPU scheduling
- Implementation change to support a simple priority queue
- Sorted items: ordered array with O(N) insert
- Unsorted items: O(N) remove & peek
Priority Queue Implementation



