Chapter 5: Linked Lists
Data Structures and Algorithms in Java
CpSc 374
General Properties of a List
-
Maintains data order
-
Time of insertion, priority, alphabetical,...
-
Recall Ordered Array & Priority Queue
-
Slow insertion O(N)
-
Had to search, then move N/2 (average) items
-
Deletion O(1) for Priority Q
- but O(N) for Ordered Array
-
List allows insertion or deletion anywhere
-
Stacks, queues, dequeues limit insert & delete
-
Priority Queue limits delete
-
Lists & Ordered arrays allow insert/delete anywhere
A list is a General Data Struct (a container for other things, perhaps)
-
Most like the ordered array
-
Problems include
-
Slow insert & delete
-
Static size limit
-
Can't make array dynamic (w/o vectors)
-
Or, amortized allocate and copy
-
Can we speed up insert & delete?
-
Have to search a linear structure for location
Why arrays again
-
They are simple
-
Basic problem is the ordering of the elements
- the connection between them is based solely on location
-
The next element is the next contiguous memory location
- previous abuts on the other side
-
This is a property of arrays --> It lets us get fast, easy "random access"
-
How does that work?

Array "pointers"
-
We can use a separate array of integers to indicate which element is next in our list.
-
Neighbor elements no longer need to be contiguous
-
They are instead "linked" by the second array
- Separate Array of Cells in Use

Insert
-
To insert an item (999) at end
- Put value in next available location: Data[newIndex] // Data[5]
- Next[last] = newIndex
- last = newIndex
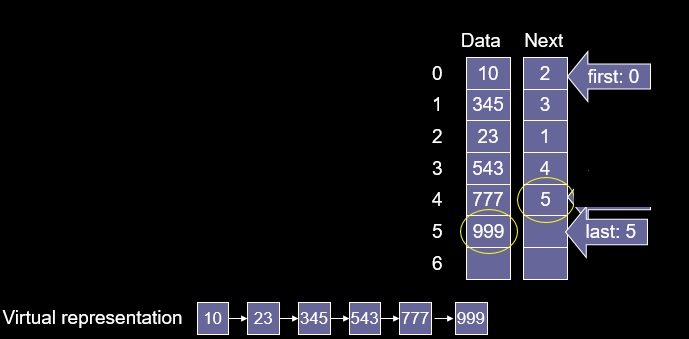
- Cost?
- Traversal just became more difficult
- Had to use a second array (of ints)
- Linked list in an array - Next[i] is our "pointer"
-
To insert an item (1) at start
- Put value in next available: data[5]
- Next[newIndex] = first
- first = newIndex

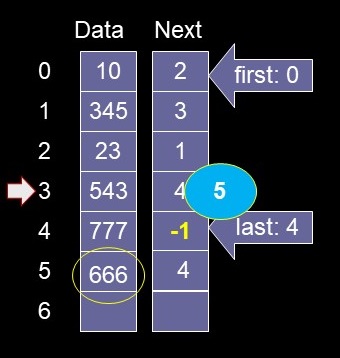
- Can we insert in the middle?
- Search for location (666)
- Let found be index of cell that will precede the new value
Current <- first
While (Data[next[current]] < v)
current <- next[current]
found <- current

Next[newIndex] = Next[found]
Next[found] = newIndex
Data[newIndex] = v
okay for 1st and last item?
 Special cases:
1. check beginning before loop
2. If (Next[current] == last) // at end
General Insert:
Special cases:
1. check beginning before loop
2. If (Next[current] == last) // at end
General Insert:
Search for location
If (Data[first] > v)
//Use insert at beginning
Current <- first
While (current != last && Data[next[current]] < v)
current <- next[current]
found <- current
If (found == last)
// use insert at end
else
// use insert in middle
Delete an element
Linked Lists ADT
- Arrays are NOT the way to go!
- Use Linked lists to implement stacks and queues
- Disadvantages:
- Have to work with references & "dynamic memory"
- Can't (easily) access items at random locations
- No [ ] operator for direct access
-

-

- Differs from array
- A Link is an object composed of
- data - probably an object reference
- next - a reference to another link object (or null
- This probably uses more space than array of int
- Java handles memory management for us
- New cells are obtained using new
- Deleted cells are returned to system for re-use
- In Java, this is implicit for an unreferenced object
- Linked list code
Special Cases
- Dealing with empty list
- Insert into empty list, or delete last node
- Insert or delete at beginning of list
- Insert or delete at end of list
- Often makes sense to think of general case first, then deal with special cases
- Working in middle of the List
- search operation (find)
- Book code -->Assume list is not empty. (What if it is empty?)
- Need to iterate through the list
- Delete a Cell
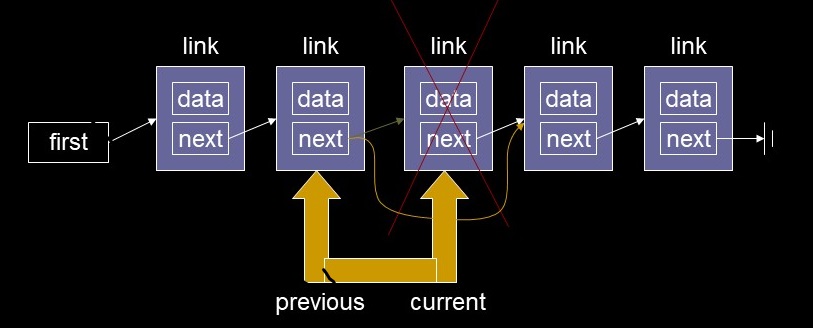
- Insert a Cell
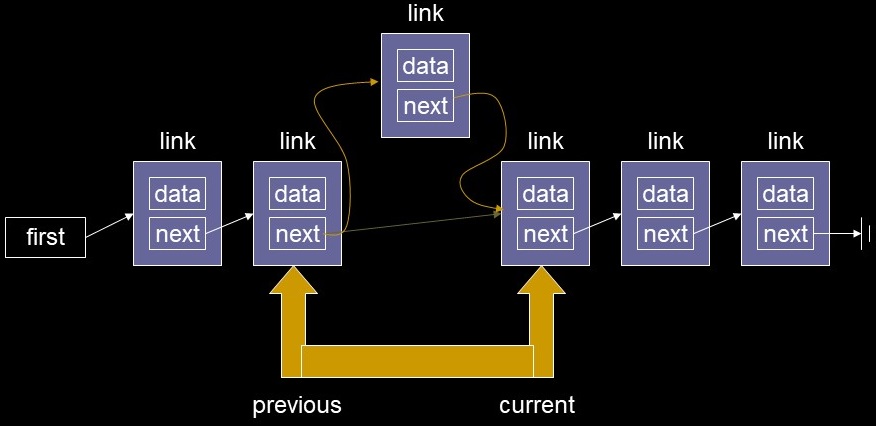
- Find a Cell

- Linked list code for
finding specified links
Using Lists for Sorting
Other liked list ADTS
- Implement a Stack
- insertFirst() & removeFirst()
- linkStack Code
- Implement a Queue?
- Need a doubly ENDED List
- Double-Ended list allows fast insertLast()
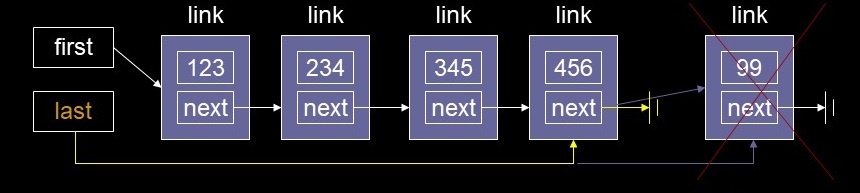
- linkQueue Code
- What if you want to traverse the list backwards?
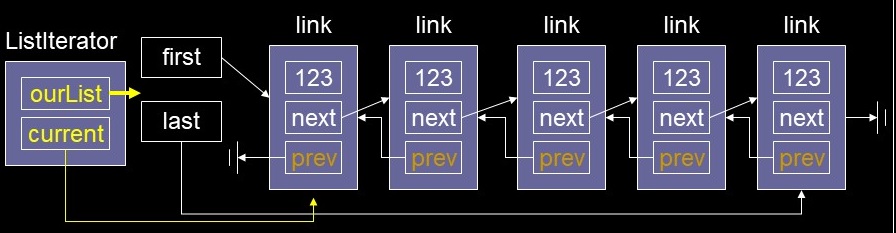
- Add a back-pointer to the Link that references the previous node in the list
- current and previous - only need one pointer now
- Doubly linked lists
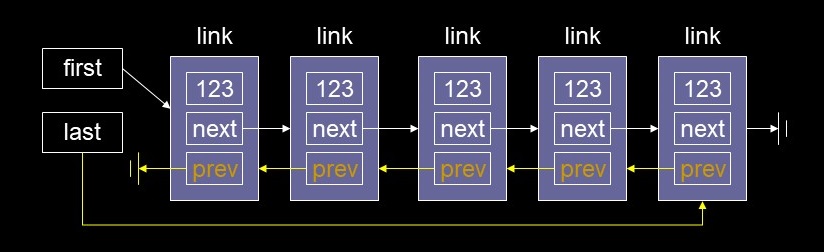
- Doubly Linked list Code
- First Last Doubly Linked list Code
- How does it affect the efficiency of the implementation?
- Insert, delete and Find are O(N)
- Need to traverse half the list on average
- Traverse list forward or backward is O(N)
- insertFirst and reomveFirst,insertLast, and removeLast are O(1)
- Can easily implement deque, queue & stack
Iterators ~ array index