Chapter 8:
Binary Trees
Data Structures and Algorithms in Java
CpSc 374
Topics
- Binary Tree Terminology
- Binary Tree Properties
- Binary Tree Efficiency
- Binary Tree Minimum Maximum
- Inserting a Node
- Traversals
- Delete a Node
- Finding Min
- Binary Search Tree
Tree Terminology

- Node - holds data or entities
- Edges - one-way connection between nodes
- Usually a reference stored in the node
- Similar to Link for linked lists
- Root - the first node & only one directly accessible (like first in a singly-linked list)
- Tree "grows from" the root
- Binary Tree - at most two edges from a node
- Path - sequence of edges leading to a node
- Parent - closest (unique) node above current node
- Child - node "below" some other node (at most two in a binary tree: Left & Right)
- Leaf - node from which there are no edges (no children)
- Length of Path - number of edges followed
- Full tree - all leaves are at same (bottom) level
- Depth - length of path from root (for tree, max length)
- Level - all nodes of a particular depth
- Root is Level 0
- Subtree - any node (the root of the subtree) and all descendent nodes
- Visit - program has direct access to the node
- Traversal - visit all nodes
- Key - data used to locate node in structure
- So, ... a linked list was a "unary" tree
Top
Binary Search Tree Properties
- BST may be empty or it will have a root node
- No node will have more than two children
- At all times, for all nodes
- The key value of left child < key value of parent
- The key value of right child >= key value of parent
- For now, assume random data
- Linked Tree Node

- Examine the Tree Class API & Data Fields from
Author's Code
- Examine the code to find a Node
Top
Find Efficiency
- For random data the tree will tend to be "full"
- Half the nodes are at the bottom level
- 1/4 at (depth - 1), 1/8 at (depth - 2), ...
- depth of tree (max path length) is O(log N)
- Equal number of nodes on left and right
- Each left-right decision splits the tree in "half"
- O(log N) average
- Data struct: binary search (w/o sorting 1st)
- Have to insert "in order"
- Worst Case (w/ BST Properties)
- Sorted data with insert-in-order
- insert: 89, 45, 22, 11, 5, 2
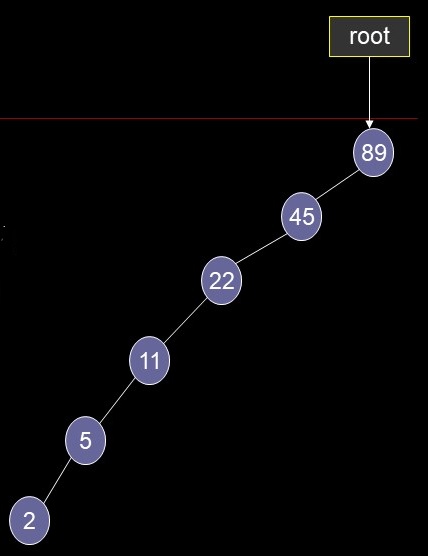
- Binary tree degenerates into a singly linked list
- find() degenerates to O(N)
- So, continue assuming random data...
Top
Finding Min or Max
-
Visualization of Binary search tree
- Minimum
parent = current = root;
while (current != null) {
parent = current;
current = current.leftChild;
}
return parent;
- Maximum
parent = current = root;
while (current != null) {
parent = current;
current = current.rightChild;
}
return parent;
- For random data:O(log N)
- Compare to priority queue or ordered array
Top
Inserting a Node
- Construct a Node
- Initialize fields
- references are null
- Check for empty BST
- Insert as root, or
- "find" the correct location
- Requires a "previous" pointer (like lists)
- Call it parent
- Examine insert inAuthor's Code
- random: O(log N)
- A traversal: "visit" each node
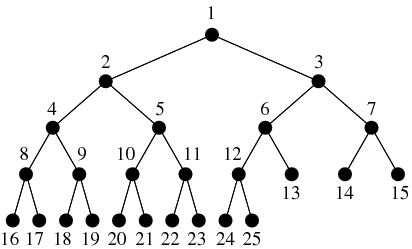
- Consider visiting by level

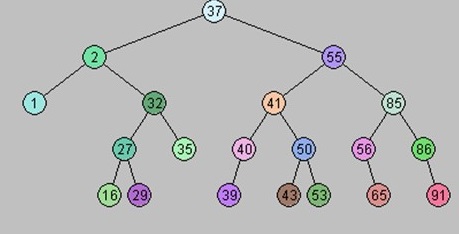
- 37,2,55,1,32,41,85,27,35,40,50,56,86,16,29,39,43,53,65,91
- Difficult!!
-
Visualization of Binary search tree
Top
Binary Tree Traversals -- Fun stuff!!
PreOrder, (recursively) visit
private void preOrder (Node localRoot) {
if(localRoot != null) {
System.out.print (localRoot.iData + " ");
preOrder(localRoot.leftChild);
preOrder(localRoot.rightChild);
}
}
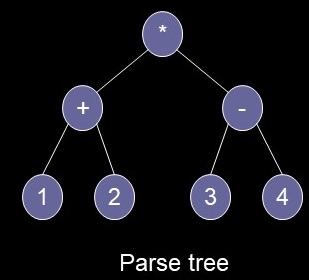
root-left-right: * + 1 2 - 3 4
mult(add(1,2),subt(3,4))
PostOrder, (recursively) visit
private void postOrder(Node localRoot)
{
if(localRoot != null)
{
postOrder(localRoot.leftChild);
postOrder(localRoot.rightChild);
// "visit" the node – do whatever with data
System.out.print(localRoot.iData + " ");
}
}
Reverse Polish Notation (RPN)
left-right-root: 1 2 + 3 4 - *
Top
Delete a node
- Case 1: Leaf Node
- Case 2: Node with one child
- Case 3: Node has two children
- Case 3a: Node has two children and successor has no children
- Case 3b: Node has two children and successor has one child
Delete a Node Case 1
- A leaf node (no children): any one of 5, 33, 53, 88
- If current is the root
- root <-- null
- Otherwise
- parent's ptr to current <-- null
- May be left or right child ...............
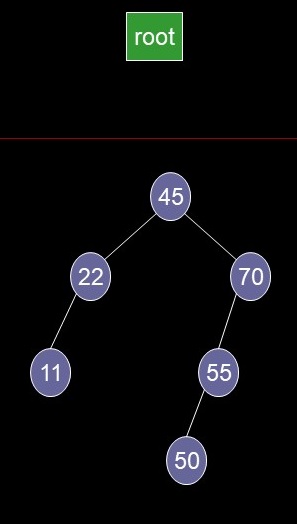
Result of Delete a Node Case 1
Delete a Node Case 2
- A node with one child (L or R): 55
- If current is the root
- root <- current's ptr to child
- Otherwise,
- parent's ptr to current <- current's ptr to child
- Child may be left or right ...........
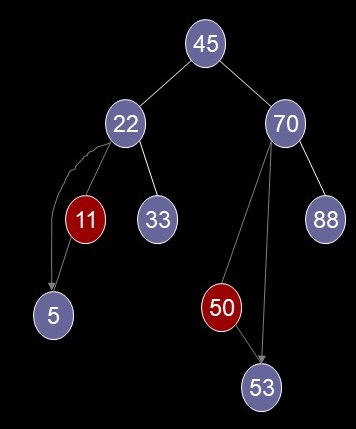
Delete a Node Case 2 (result)

- Delete a Node Case 2 (again)
- A node with one child: 11, 50
- If current is the root
- root <- current's ptr to child
- Otherwise,
- parent's ptr to current <-
current's ptr to child
- Child may be left or right
...... .. Delete a Node Case 2 (result)
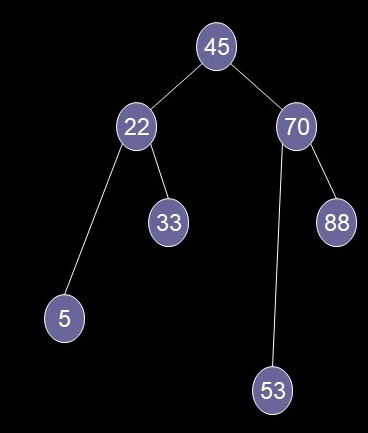
Delete a Node Case 3
- The node has two children

- Replace 22 with 33 (left side)
- Replace 70 with 88 (right side)

Successor
- Need to pick a replacement
- Find the successor to current node (current is node to be deleted) -
Smallest key in right subtree
- Note that the smallest key in right subtree will be a leaf
- Find minimum in right subtree
- a. Step right
- b. While there is a left child
- --- Step left
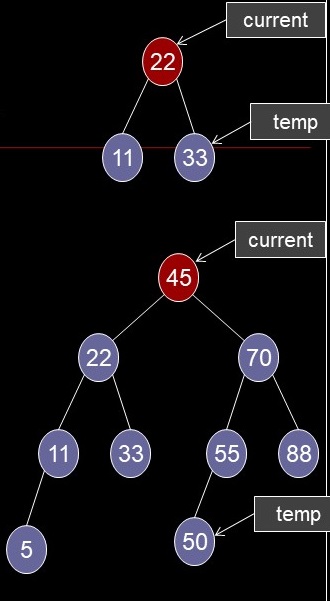
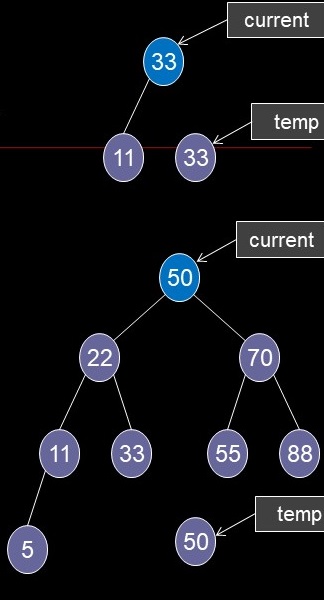
- Delete a Node Case 3a
- Successor has no children
Example
- 22: successor is 33
- 45: successor is 50
- temp <- successor
- Delete successor
- See case 1 (successor is unlinked, not actually deleted)
- current.key <- temp.key
- current.data <- temp.data
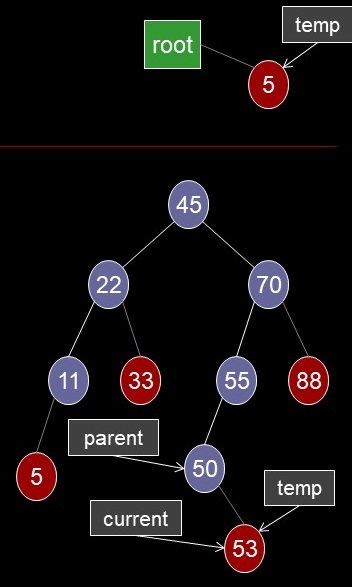
- Delete a Node Case 3b
- Successor has one (right) child
- 45: successor is 50
- current <- successor
- Delete successor
- See case 2 (successor is unlinked, not actually deleted)
- current.key <- temp.key
- current.data <- temp.data

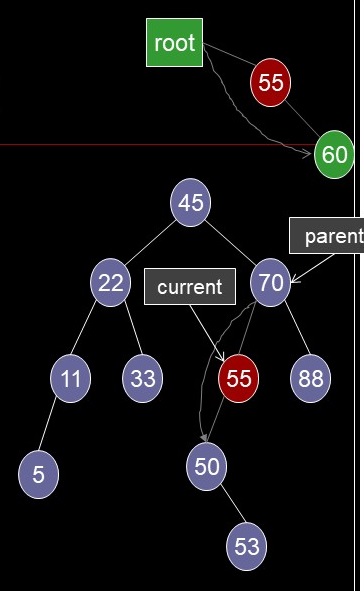
- Delete a Node Case 3b (part 1)
- Successor has one (right) child
- 45: successor is 50
- temp <- successor
- Delete successor
- See case 2 (successor is unlinked, not actually deleted)
- current.key <- temp.key
- current.data <- temp.data
.......... Delete a Node Case 3b (result)

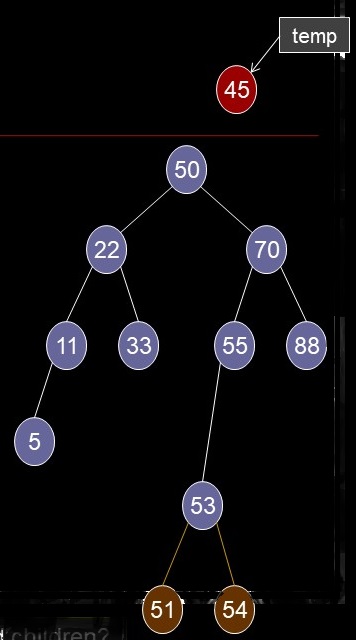
Tree vs. Subtree
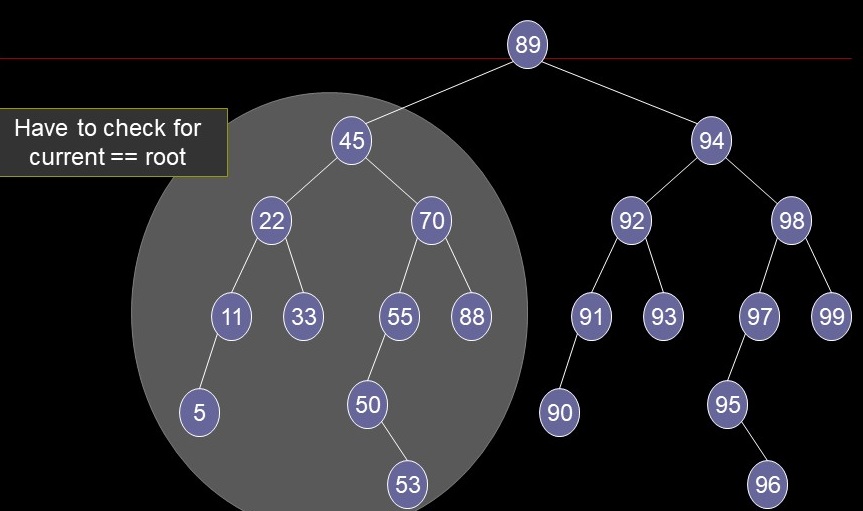
Efficiency Revisited
- Calling the delete routine recursively for case 3 is guaranteed to result in case 1 or 2
- However, this requires another find operation
- We skipped the find step when looking at delete
- Assumed we knew current & parent
class Pointers {
public Node parent;
public Node current;
}
Finding a Node Revisited
public Pointers find2 (int key, Node myRoot)
{
if (myRoot==null)
return null;
Pointers p = new Pointers();
p.current = myRoot;
p.parent = null;
while(p.current.iData != key) {
p.parent = p.current;
if(key < p.current.iData)
p.current = p.current.leftChild;
else
p.current =p.current.rightChild;
if(p.current == null)
return null; // not found
} // end while
return p; // Parent & Current
}
Finding Min or Succesor
public Pointers findMin2 (Node myRoot){
Pointers p = new Pointers();
p.current = myRoot;
p.parent = null;
while (p.current.leftChild != null) {
p.parent = p.current;
p.current = p.current.leftChild;
}
return p;
}
public Pointers getSuccessor2( Node myRoot){
Pointers p = new Pointers();
if(myRoot.rightChild == null)
p.current = myRoot;
else
return findMin2(myRoot.rightChild);
return p;
}
Worst case (linked list) for all ops: O(N)
Delete
public boolean delete(int key){
Pointers p = find2(key, root);
return delete2(p);
}
delete calls find2
may travel to bottom level, or stops in the middle & calls delete2
delete2 call getSuccessor2 (1 level) calls findMin2
may travel to bottom level
Still O(log N) average
boolean delete2(Pointers p)
Already knows
p.current
p.parent
When node has two children
Call getSuccessor2()
Call delete2() on result
Does not call find or find2
Replace node key & data
Tree in an Array
Root: index == 0
Given a node's index:
leftChild == 2*index + 1
rightChild == 2*index + 2
Parent == (index - 1) / 2

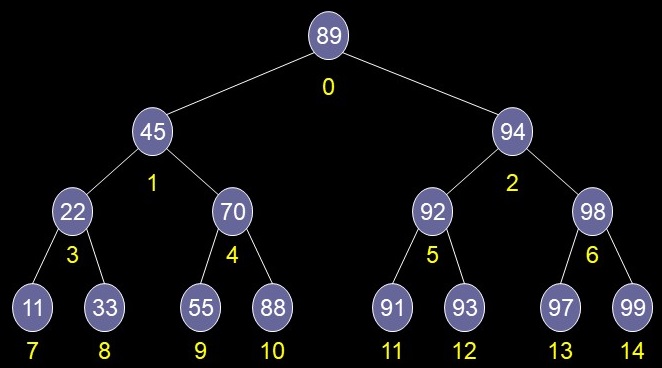 Why use an array?
We just gained "back pointers"...
like a doubly-linked list, but no pointers (or references)
No longer need parent (previous)
(if useful) gained direct access to any node
Why use an array?
We just gained "back pointers"...
like a doubly-linked list, but no pointers (or references)
No longer need parent (previous)
(if useful) gained direct access to any node
 Array => No Pointers
May have a "sparse" array
Add a level : double the size of the array
"half" the new nodes empty
Array => No Pointers
May have a "sparse" array
Add a level : double the size of the array
"half" the new nodes empty

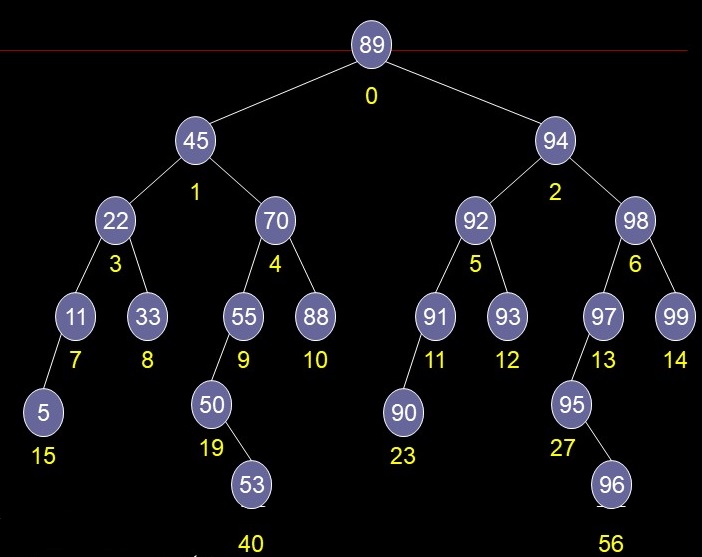
Top
BST Comparison
- Ordered array:
- Fast binary search
- Easy traversal
- Slow Insert & Delete
- Linked List:
- Fast Insert & Delete
- Easy traversal
- Slow search
- BST - random data
- fast binary search
- recursive traversals
- in-order: sorted output
- pre-order & post-order useful in some apps
- fast insert
- Delete op is complex
- BST - sorted data
- A complex linked list
- Using a BST to sort
- Insert N items into tree
- inOrder traversal
- copy back to array
- Random data (average & best):
- O(N log(N) + N)
- Worst case:
- O(N2 + N)
- Bad choice for both space and time efficiency.
- What if data is already in BST?
Top