Using Gravity to Navigate the Internet and other Graphs

Using Gravity to Navigate the Internet and other Graphs

David Dailey, Deborah Whitfield, Jake Weidman, Grant Denmead

ABSTRACT
Water flows downhill, and though its route is not always the shortest path to the sea, gravity helps it to find a path. Might we find some analog to gravity in more abstract metric spaces, like graphs, that would allow a simple algorithm to find shortest paths to arbitrary destinations? How little local information is needed at a node in a particular graph to determine to the path to a given destination?  Gravitational analysis of even very small graphs proves too difficult to analyze by hand, so a JavaScript program was written to perform calculations of gravitational flavorings.  This code was then integrated into the Grapher program presented at SVG Open 2009. (1) We then generate artificial web sites based on graphs of differing gravitational properties. The paths that subjects take through a variety of graphs has been analyzed. The experimental results show that cues of gravitational flavoring can assist subjects in exploring non-Euclidean spaces by reducing the number of steps taken in their exploration.

1. Introduction

To what extent does a topological or graph theoretic solution to a problem predict what humans might actually do when faced with problems of navigating graphs like web sites, floor plans, or the entire internet? While gravity and magnetism are cues that can help us chart courses for chosen destinations, might some analogue to these “field effects” be found in arbitrary, non-Euclidean metric spaces, like graphs?

In order to think about how humans might navigate through abstract spaces, consider how they might navigate ordinary spaces, as on the surface of the earth. A bit of introspection suggests that humans rely on several things for navigation including landmarks (familiar things, especially those that can be seen from many places) and a “sense of direction.” This sense of direction might include knowing what directions are backwards, forward, left and right and especially up and down; humans come with a rather direct perceptual awareness of up and down based on gravity. The sense of direction might also be augmented by reasoning based on such notions that three right turns might head back to the starting point, or that after moving 20 miles north and 20 miles west, then heading southeast might return to the starting point. Such “calculated” or “augmented” awareness of direction might seem to rely upon intellect, or even tools like compasses or astrolabes to refine our measurements of current location and destination. Indeed the study of human cognition as it relates to mapping and navigation dates back to at least 1979 (8) and has been investigated (9,10) in the context of gender differences and familiarization with new operating systems.

It has been shown that certain species of birds and insects rely not just on gravity for navigation but also on magnetic “sensors” that are responsive to the earth’s magnetic field. (11) That is, we may think of magnetism and gravity as “field effects” like a vector bundle flavoring each point of the space we inhabit.

To what extent might these concepts of field effects or directional flavoring be generalizable across spaces of radically different metric and connective properties than our familiar Euclidean ones?

This paper introduces the concept of gravitational flavoring, in which each of a graph’s nodes are numbered in a way that reveals the shortest path from source to destination for all pairs of nodes. The utility of such a technique is seen when one considers that these concepts are more directly applicable to the large and important graphs that have come to grace the landscape of the human intellect in recent years; individual web sites and the World Wide Web itself. These are, of course, graphs (directed or bidirectional if one considers the “back” button in the browser). The pages are nodes and the hyperlinks are edges in graphs that may vary from a handful of interconnected pages, to in the case of the web itself, hundreds of millions of pages.

While search engines (historically from Yahoo, through Lycos and Alta Vista to Google and Clusty) have sought to provide guided tours of those realms to their visitors, they have not been in the business of distributing maps. Maps might be too egalitarian, and the value of the tour guide might then diminish. Or perhaps it is simply that mapping that content, using any sort of a proximity metric, has just defied either the horsepower or the imagination of the would-be mapmakers. Perhaps it is because the general constructs of navigation in these abstract spaces have yet to be defined or investigated. So this is what we are interested in: given space, in some of its most non-Euclidean incarnations, and given humans who find themselves in those spaces:

a)  How do humans get around in those spaces? In the best cases, how might they get around in those spaces?

b)  How might we either redesign or redecorate (using better signage) those spaces so that human navigation might be improved?

Before discussing the technique and its possible application to building web sites, a bit of mathematical background is needed.

2. Background

The underlying principles of this paper pertain to some rather new and provocative mathematics. We will begin with a discussion of the basic concepts, using just enough formality to introduce the concepts to those both with and without mathematical sophistication. For the latter group, please bear with us, as we promise to become more intuitive after the basic ideas have been set forth.

Several centuries of experimentation with Euclid’s fifth postulate (and the unsuccessful attempts to reach a reductio ad absurdum if it were denied) finally came to fruition in the 1800’s in the non-Euclidean geometries of Bolyai, Lobachevsky and Riemann. Bolyai concluded, “It is not possible to decide through mathematical reasoning alone if the geometry of the physical universe is Euclidean or non-Euclidean." (12) These geometries explored the properties of such constructs as “geodesics” in combination with other systems of geometric axioms. Many are indeed quite practical geometries, having importance in fields ranging from the physics of relativity to geography.

As noted by Clemens, (2) another way of creating non-Euclidean geometries is to “simply introduce a distance function other than the Euclidean distance.” The Minkowski metric (3) allows a generalization of distance in spaces that are nevertheless Cartesian (having axes) and by doing exactly that. The distances between points being are based on simple formulas of their positions on those axes. But a more theoretical generalization comes from the mathematical concept of the metric space, a relatively intuitive axiomatization of the concept of “distance” as it has been used by humans throughout the centuries (both with and without the theories of mensuration developed by the Egyptians for regulating agriculture). Specifically, a metric space is defined by a set of points in which four things (axioms) are true:

1. Between any pair of points there is a pathway, and any pathway can be measured by a distance: a non-negative real number.

d(A,B) ∈ [0,∞)

2.  The distance between two points is zero precisely when they are the same point.

d(A,B)=0 iff A=B

3.  Distance is independent of the direction of travel: for any two points A and B, the distance from A to B is the same as from A to B.

d(A,B)=d(B,A)

4.  In going to C from A it is no shorter to go through B than to go directly. This is the familiar “triangle inequality.” For points A, B, and C and distance function d,

d(A,C) ≤ d(A,B) + d(B,C)

If we further restrict the distances to be integers, then we have what can be called a discrete metric space. It is straightforward to show that each graph (finite or infinite) is a discrete metric space (using the standard graph theoretic concept of the distance between nodes being the minimal path-wise distance between them) . Any standard treatment of graph theory such as [4] or [5] will provide the needed background.

Furthermore, it turns out that any discrete metric space can be precisely modeled by a graph. If we are given the space, namely its points and their distances, then we may construct a graph in which the points of the metric space are nodes of the graph and for which the graph theoretic distances between the nodes exactly match the prescribed distances. [6] seems to be the first formal investigation of this fact by exploring the properties of the smallest graph that might model a given metric space.

Given this rather interesting notion that spaces can be modeled by graphs, it becomes, in some sense, natural to consider the nature of the physics that might be enabled in such abstract theories of spaces without axes. A broad treatment of many of the graph theoretical issues of distance may be seen in [7].

While the applications of abstract graph theory to physics are entertaining to contemplate, the concept of gravitational flavoring is the focus of this paper.

3. Gravitational Flavoring

When the term graph is used in this paper, we are referring to connected, bi-directional or un-directional graphs.

Definition 1: A flavoring of a graph on N nodes is an assignment of the integers 1 to N to the nodes so that each node has a unique number. Those numbers are called the gravity values of the flavoring. The concept is virtually the same as a labeling: each node is given a unique label; a flavoring is essentially a labeling by the integers that will be used for navigational purposes.

Definition 2: A graph on N nodes is gravitational if there exists a flavoring of the nodes such that a shortest path will be found (between any given pair of nodes) by a simple greedy algorithm that chooses the next node from among those neighbors that have gravity values closest to that of the destination node.

Remark: We will use the terms gravitational, gravitationally flavorable, or flavorable with one-dimension of gravity interchangeably. Definition 3 will clarify the meaning of “dimensions of gravity.”

Examples:

The following graph on 42 nodes is gravitational, with the numbering of the nodes representing one of its flavorings. The use of gravity in traversing paths between two pairs of nodes is illustrated by way of example.

Figure 1: A grid graph comprised of the product of two paths: P₇ x P₆.

Traveling from node 5 to destination node 30 proceeds thusly: Node 5 has three neighbors: nodes 4, 6 and 10. Node 10 is numerically closest to the destination of node 30
(since |30-10|<|30-6|<|30-4|), hence the path begins by choosing node 10 next. From there, node 19 is closer to node 30 than either of node 10’s other neighbors (nodes 5, 9, and 11), hence, node 19 is the next node chosen. Similarly, the next node will be 24. From node 24, we have choices of nodes 19, 23, 25, and 33. Node 25 is 5 units of gravity from the destination of node 30, so node 33 is closer. From node 33, the path proceeds “downhill” to nodes 32, 31 and finally to node 30. The gravitational path from node 5 to node 30 is thus (5,10,19,24,33,32,31,30): a path of length seven. The reader may verify that the path suggested by the flavoring is indeed a shortest path (there is no shorter path traversing the edges of the graph).

Traveling from node 37 to node 16: The path suggested by gravity is (37, 34, 23. 20. 19, 18, 17, 16) . Obviously there is no shorter path (although there are several paths of equivalent length!), so gravity reveals a shortest path in this case as well.

The reader, if interested, should observe that proving that this flavoring generalizes to all pairs of nodes is not difficult. We will not aspire to that level of formality, though, in this paper. It is exactly when a flavoring of this sort motivates “perfect navigation” between all pairs of nodes that the graph is called gravitational.

Clarification: It should be noted that for a graph to be gravitational it is required not only that a shortest path “may be found” but that it “will be found”. That is, if the simple search has two choices that are gravitationally equidistant from the destination, then both must yield shortest paths. We cannot rely upon oracle algorithms to make lucky guesses when two choices present themselves.

Example : A graph which is not a gravity graph.

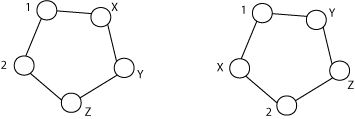
Figure 2:  the cycle on five nodes. At left figure 2a, at right figure 2b.

The cycle on five nodes, known as C5, cannot be flavored so as to motivate proper navigation between all pairs of nodes. Here is the reason: We have two possibilities for the labeling of nodes 1 and 2. Either they are adjacent or not, and owing to symmetry we have only the two cases shown in Figure 2a and Figure 2b. In 2a, consider where to put the label “5.” We cannot put it at X, since then it would not see the shortest path from 5 to 2 (through 1). We cannot put 5 at Z, or else it would not see the shortest path to 5. Therefore Y must be labeled 5. This leads to the problem though, that wherever we place the label 3, it will draw the path from 5 to it in pursuit of either 1 or 2. For one of those, this will fail to find the shortest path.

In Figure 2b, the label of X cannot be 5 since 1 would not see the shortest path to X. If 5 were at Y, then Z will not see the shortest path to 1. And finally, if 5 were at Z, then Z will not see the shortest path to 1, being drawn instead to 2.

We state the following without proof, though the proof is relatively easy for those who enjoy proofs:

Theorem: If a graph G is gravitational, then the product P_n x G is also for any simple path P_n on n nodes. The proof follows by labeling the nodes in each of the copies in ascending order for odd numbered copies of G and in descending order for even copies of G, as illustrated in Figure 2, which also illustrates both an example of the theorem and of the labeling used in its proof.

A sample of such a graph is seen in Figure 4 (later in this paper) the fourth graph in the second row and in the results section as 8d_flavored, Ambassador.

Theorem: If G, a graph on N nodes, is gravitational, then we may make a new graph on kN (the product of k and N) nodes as follows: Make k copies of the graph G. Temporarily label the nodes in each copy G_i with the flavorings from the gravitational flavoring of the first copy, as shown below. The gravitational earliest node in G_j becomes n_j,1 and so forth. Now stitch the copies together so that n_j,N has one line added connecting it to n_i+1, 1 for each i<k. The resulting graph is gravitational, as is easy to verify, by flavoring the nodes in ascending order across the copies.

Figure 3: Stitching four copies of the gravitational graph, K5 – line, together into a new gravitational graph on 20 nodes.

Definition 2: A k-dimensional flavoring of a graph on N nodes is an assignment of k numbers to each node of the graph so that the j-th values of all the nodes form a permutation of the numbers 1 through N. For a node p, we can write this as f(p)=(p₁,p₂,p₃,…,p_k)

Example

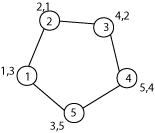
Figure 4: A two-dimensional flavoring of the graph C5

Note that both the x and y dimensions offer flavorings that consist of permutations of the numbers 1 through 5.

Definition 3: Given a k-dimensional flavoring of a graph, the flavor-distance between two nodes is given by the Minkowski r-metric:

d(p,q) = ( S ( | p_i – q_i | ^r) ) ^1/r

We have left the particular metric here open to the reader’s favorite distance formula. Those who like Euclidean distances will use r=2, as we do below. For ease of computation, though, we might use the city-block metric in which r=1.

Definition 5: A k-dimensional flavoring of a graph is called gravitational if a walk between any pair of nodes has the following property: By choosing the next node so as to minimize the flavoring distance between current position and destination, we will succeed in finding a shortest path within the graph between those two nodes.

Example: Using the graph and its two-dimensional flavoring from the illustration in Figure 4, we observe the following distances between pair of nodes (squared distances are presented for ease of presentation):

Note that the following paths suggested by the above flavoring are all shortest paths. Hence, C5, while not being gravitationally one-dimensional, is indeed gravitationally two-dimensional. We may think of these two dimensions of field effects as being like gravity and magnetism.

To navigate from N1 to N4, we examine the two nodes that N1 is connected to (N2 and N5) and select the node that has the shortest distance to the destination node, N4. Since N2 to N4 has distance 18 and N5 to N4 has distance 5, N5 is selected. The process continues from N5. Since N5 is connected to N4, we have the path: N1, N5, N4.

All of the paths are given in this table in abbreviated form: (N1,N5,N4) is given as (1,5,4).

Note: It is interesting to observe that the above flavoring of C5 does not seem to motivate perfect navigation if we use the city block metric instead of the Euclidean, because of certain diagonals appearing to be equidistant with certain neighbors.

We must confess to knowing very little about which graphs are and are not gravitationally two-dimensional. .

Among our current questions on the topic are:

-Is each graph on N nodes is gravitationally N-3 dimensional?

-Are all graphs on five nodes are gravitationally 2 dimensional?

-Is any graph which is gravitationally k-dimensional is also gravitationally k+1-dimensional? It would certainly stand to reason that it should be, but our definition of multidimensional gravity, at present, does not allow the algorithm to simply ignore certain dimensions of influence.

From a graph theoretic perspective, only adjacent nodes from the source node can be examined to determine which node to visit next to find the shortest route to the destination node. From an Internet user’s perspective, what link should be followed on a page to get to a desired page the fastest?

4. Gravity Calculation Software

Software was developed for the creation of web sites from graphs, regardless of gravitational flavoring. This process first began with a non-graphical server side engine that accepted and generated XML for graphs to determine if a graph was flavored and, if not, to produce a flavoring if one existed. Next, this code was embedded into Grapher, an SVG tool for creating and modifying graphs. Finally, Grapher has the option to generate a website from a graph in which the inter-connectivity of the website matches exactly that of the graph designed. This option has been improved considerably over its previous incarnation.

THE ENGINE

Gravitational analysis of even very small graphs proved too difficult to analyze by hand, so a C program was written to perform calculations of gravitational flavorings. In order to determine if a graph could be flavored in one dimension (i.e., a single integer value) and thus was gravitational, two steps needed to be performed. First, the shortest path for all pairs of nodes had to be calculated. This calculation used Floyd’s algorithm (13) and maintained the actual paths as strings. Next, for each permutation of integers over the number of nodes, that ordering was checked to see if it was indeed a gravitational flavoring. All permutations were evaluated so that multiple correct flavorings could be found if they existed.

Calculating the shortest path between all nodes can be performed in O(n³) operations. However, all possible permutations is by necessity an O(n!) algorithm. The original gravity calculation engine software was written in C for speed. It was quickly determined that a non-textual (i.e., graphical ) program was needed in order to visualize the graphs and investigate possible path information. The C program was translated from C to Javascript and SVG and embedded into Grapher.

EXISTING GRAPHER SOFTWARE

Grapher was developed by several students at SRU and was presented formally at SVGopen 2009 (1). Grapher is a tool written in SVG and Javascript that permits the user to draw a graph using point and click (i.e., no edges need to be drawn). The user can import and export graphs, select nodes and/or edges, edit graphs, copy graphs, etc. In essence, the original tool was used as the basis for gravitational flavoring.

COMBINING GRAVITY INTO GRAPHER

The C code for calculating the shortest path between nodes was translated with ease into Javascript although paths were not stored as strings. The recursive calculation of permutations to verify if a permutation was gravititational was also converted with ease. But, the recursive nature of the permutation code becomes too much for the browser to handle when there are 9 nodes or more in the graph.

One of the first modifications made to the Javascript code was to simply check if a given flavoring is gravitational or not. This verification does not require all permutations to be computed, but simply verification that the numbering is indeed gravitational.

GENERATING WEB SITES FROM GRAPHS

We then generate artificial web sites based on graphs of differing gravitational properties. The nodes of the graphs become web pages in which the edges are represented as hyperlinks leading to adjacent nodes. Hyperlinks can contain hints such as a color, an object, a word, or the gravitational value. In order to investigate how human subjects navigate a web site, a game was created where web pages are rooms and users attempt to navigate the graph by visiting all rooms or by finding a “prize” while avoiding obstacles.

In order to create environments for test subjects to navigate, we decided that it would be more efficient to create an environment constructor, which we called the HTML Constructor, to randomly create environments for us based on a number of different variables. This program provided the flexibility to quickly create many different looking environments for test subjects based even on similar or dissimilar graphs created in the SVG Grapher program.

The HTML Constructor works by interfacing with a graph structure that is created in the SVG Grapher program. Among the various export options found in Grapher, the ability to construct a website as an export feature has been added. When activated, Grapher sends information detailing all nodes and their connections to the HTML Constructor. There, a number of options are available to the person creating the website including page color, text/hyperlink color, the option to place images, the option to create a “Landmark Page”, random word generation, hyperlink/button ordering options, options for node labels, and the option to include empty space for nodes that are not visible from the current node that the test subject is on. All of these features provide the website creator with a good degree of control over what clues they want to give the user regarding the site’s structure.

The website itself is constructed based on the user’s input, and has its path name scrambled to prevent the end-user of the website from learning anything about its structure by using its file name. The visual content displayed to the user is dynamically created SVG, and the code at work behind the scenes is primarily PHP. When first entering a new “maze”, a small amount of client-side JavaScript adjusts the separation between buttons on the screen to optimally fill the user’s screen. Underneath the SVG, when a user first enters a structure, we check to ensure that the user has not completed the website before. A similar check is performed again before the user’s data is submitted to the final data file. If the user has not previously completed the website, a session is started containing the user’s IP address, the current graph (website), and the user’s path (from node to node) and time (in seconds are recorded). We also “timeout” the user if he or she does not leave the page for a period of a few minutes or more. In this event, the user is locked out of that particular website and will be unable to re-enter. As the user traverses the structure, his or her path is maintained as well as departure and arrival times at each page in the site. Once the user has navigated the entire structure, a message is displayed to direct the user to return to his or her starting page. Upon completion of this task, a PHP script again checks the “validity” of the user’s data against the current data file. If this check is passed, their data is submitted, and the user is redirected back to the splash page and allowed to complete another structure if they so choose.

5. Experimentation and Results

Recall that the overall goal of this work was to determine if gravitationally flavored graphs were easier for human navigation. Thus, websites based on underlying graphs that are both flavorable and non flavorable need to be traversed by humans.

EXPERIMENTS

Many experiments were considered for the first trial, however, it was quickly determined that more advanced experiments first needed to have the basic question of “Does gravitational flavoring make a difference in navigation?” answered. Thus, several design issues had to be considered:

• Graph size
• Number of graphs in the study
• Test subject pool
• Types of cues on web pages
• Type and placement of “door ways” between pages
• Sophistication of the “game” design
• Data collected

Graphs of sizes 8, 12, and 16 were decided to be appropriate since they were not too small to be quickly traversed and not likely to be memorized. Four graphs of each size were created that were flavorable and each of these 12 graphs were modified by adding and/or removing edges so that the graph was no longer flavored. Each of the gravitational graphs was also flavored with a non-gravitational flavoring, so that 36 (3 sizes x 4 examples x 3 treatments) labeled graphs were actually used. Figure 4 shows a collage of the graphs used in this study.

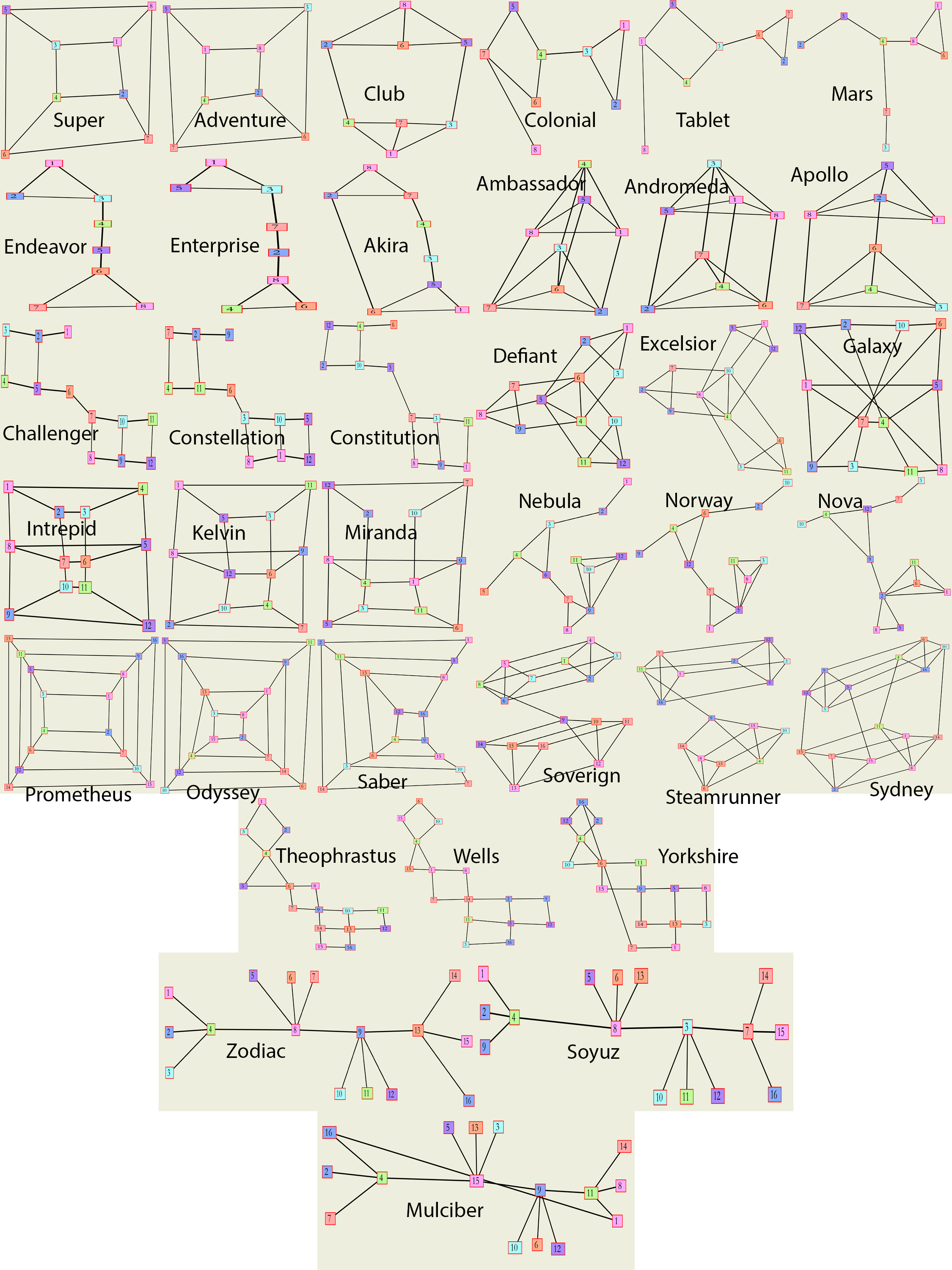
Subjects: The experiment was advertised through several social media sites: Facebook, Google+, svg-developers, and advertised to some of the students enrolled in computing courses at SRU. The identity of the users is unknown. Furthermore, the site advised that the participant was to be 18 years or older. In all, our experiment attracted 35 different participants. (This is perhaps just an estimate since it is based on differing IP addresses.)

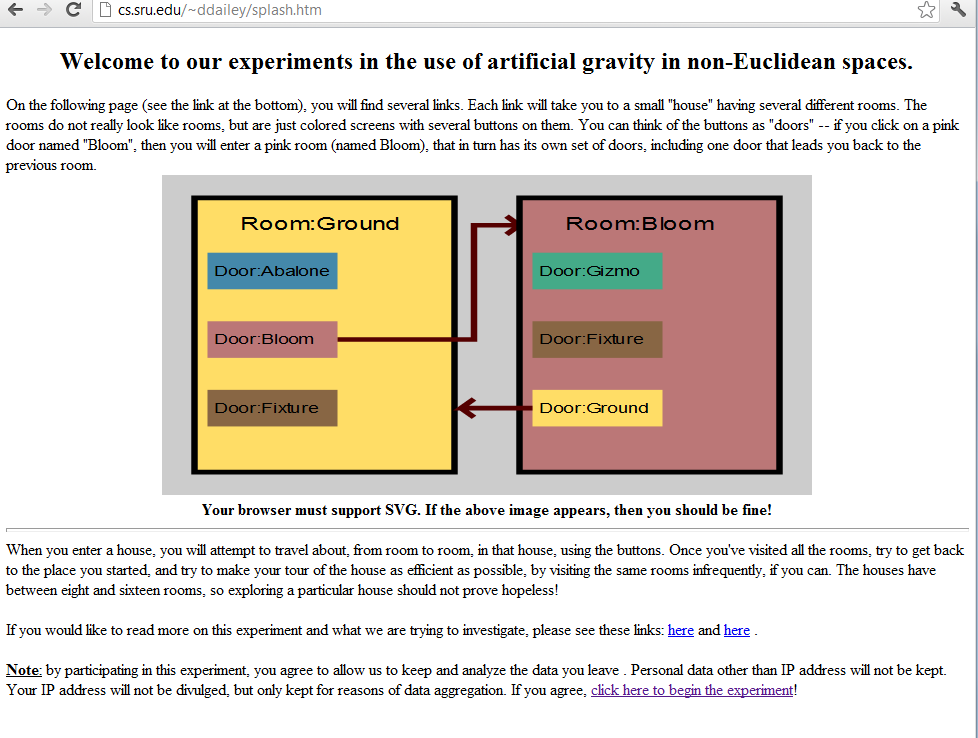
Instructions: The instruction page may be seen at http://cs.sru.edu/~ddailey/splash.htm where a picture of the task is presented:

Stimuli: On each created site, a node was represented as a page consisting of a background color and a word. Each link to the next page consisted of a rectangle with the next page’s word in the color of that page.

For each gravitationally flavored graph, two web sites were created: one with the numeric flavoring showing and the links to other pages in order (using the gravitational flavoring); and a second without the numbering showing and the links in random order. For each non-flavorable graph, a web site was created with random link orders.

Subjects were placed in a random place within the graph and asked to navigate to every page and then return to their starting place. Each time a subject visited the splash page the subject was placed in a random graph. However, IPs were maintained so that a subject could not re-visit a site after completing it.

The experimental setting: The volunteers used SVG enabled web browsers and could have done so from literally anywhere on the Web. We do not know if they were at home, on cell-phones or in public workstations.

RESULTS

The 35 participants completed a total of 156 solutions of the 36 graphs used in the study. They spent a combined total of 18,364 seconds (117.7 seconds per solution with a standard deviation of 121.8 seconds) and made a total of 4,285 moves (transitions from room to room), representing an average of 27.5 moves per solution (standard deviation of 16.5).

It is worth noting (as shown from the standard deviations) that the variability associated with these solutions was very high. The range of times spent on graphs was from 12 seconds to 875 seconds, while the range of moves per graph was less daunting: from 8 moves up to 80 moves. A casual perusal of the data revealed that some of the graphs that took the most time, were in fact not producing the highest number of moves. The correlation (Pearson’s r) between these two figures (as aggregated across the 36 graphs) was only 0.53. This correlation suggests (given the uncontrolled nature of the experimental setting) that oftentimes the subjects may have been distracted, and called away from the task by various distractions such as phone calls. We could have teased this out a bit more by looking at the move to move times to see if the delays showed any patterns related to the graphs themselves, but it appeared that the more reliable data here is likely to be the move data. As such, we spent far less time analyzing the time data. Both, though, are shown below as a function of the graphs.

Table 1 - Experimental Data for All 36 Graphs

* Variance is meaningless with only one data point.

Table 1 shows, for each of the 36 graphs, the mean and standard deviations for both number of moves and average time (in seconds) for each of the solutions of the graphs. The data has been sorted by the average number of moves to completion.

What is relatively obvious from the table above, is something that would be obvious before running the experiment: larger graphs generally take more steps to complete.

This conclusion is borne out by the following table (2):

Table 2 - Comparison of Larger Graphs

This shows that the number of moves per solution rises at slightly more than two visits per node, with the larger graphs clearly requiring more time and effort.

The more interesting comparison, of course, is between the three different types of gravitational effects. These data can be viewed in Table 3.

Without performing significance tests the Analysis of Variance (ANOVA) would be a rather complex mixed model with subjects (a random-effects variable) being crossed by graph prototype (another random-effects variable) and crossed by Graph Size and Gravity (both fixed effects) and graph prototypes being nested in Graph Size and crossed with Gravity. Though we didn’t perform such an ANOVA, the data would suggest the following:

• The main effect for Graph Size (significant)
• The main effect for Gravity (significant)
• The effect of Graph Prototype (significant). Some graph types are easier than others.
• The Graph Size by Gravity Interaction (insignificant)
• The Graph Prototype by Gravity interaction (likely insignificant owing to the large variances involved)

Post-hoc tests (such as Tukey’s) on the main effect of Gravity, would likely show that flavoring matters but that we are unable, from this experiment, to differentiate from the flavored and the unflavored graphs. That is, the slight difference observed between the means here is likely to be insignificant.

Various effects due to individual differences (such as Subjects by Graph Size and the Subjects main effect – testable since Graph Prototypes can be treated as a random effects variable) are also likely to be significant though of little overall consequence to the study at hand. Individual differences in such a task are not unexpected!

Overall, the main question of the experiment was answered affirmatively: providing gravitational cues to subjects as they explore a non-Euclidean space is helpful toward reducing the number of steps it takes to explore that space.

6) Summary and Future Plans

This paper introduces a new concept of gravitational flavoring of graphs that can be used for some graphs to determine shortest paths between sources and destinations. This definition is formalized and theory showing how to create larger flavored graphs from small falvored graphs is given. Existing SVG graphing software was extended to include the calculation of gravity in graphs, and determining whether a graph is gravitationally flavored. The software’s generation of a website from a graph was improved. And websites of given topology and gravity were produced. These websties were navigated by users and the results of the subjects were analyzed. It was determined from these tests that gravitational flavoring does reduce the number of steps needed to explore a web site.

Future plans for this work are quite extensive and include modifications to the software and further theoretical work. During experimentation, several flaws in the software for determining gravity were found and are currently being corrected. The largest issue with the software is in the size of the graphs that can be used. The recursive calculations of permutations quickly become too deep. As such, the software will be modified in a variety of ways including a non-recursive solution for permutation calculation.

We identified several improvements to the HTML Constructor. The first feature that will be added is the ability to import an XML file into the constructor program to create a website. Currently, the constructor must be accessed through SVG Grapher. Many times, graphs would be created using the SVG Grapher, and would then checked by multiple team members by saving the graph as an XML document. To create a website using this graph, the XML file would have to be re-imported to Grapher in order to access the constructor. In the second version of the HTML Constructor will enable XML import.

We would like to add a live, reduced functionality version of the SVG Grapher program to the HTML Constructor. This would give the website creator the ability to have a view of the graph he or she is working on while determining the desired features for the site. The reduced function Grapher would also allow the user to change node labels and connections in real-time, allowing for a greater flexibility to create websites. Along with the SVG Grapher being partially present in the new HTML Constructor, we would also like to implement the ability to preview a website before it is actually created. This would give a finer control to the user and would prevent tedious experimentation, creating and deleting of later un-used websites. This software could also be quite in data analysis and visualization.

We have also considered such things as allowing the user to track their position from a topical view of the website, or at least to see a list of nodes currently visited and unvisited as in a kind of Head-up display (HUD). This would give the end-user a different perspective and perhaps give them different thoughts on how to navigate the structure they are in.

Beyond these main features, other smaller options may be added to control page content. An example of this may be the ability to construct a site using a custom set of words specified by the user. As we continue to develop the program, we will surely encounter other areas in which the original code can be improved upon to create superior testing spaces.

In addition to software changes, a more complete study and data analysis needs to be made that include:

• · Determining if problems occur within the graph to make it difficult for a subject to learn the graph (i.e., easily navigate)
• · Calculate node by node visitation frequency to determine which paths are most frequently used and which are not
• · Further develop two-dimensional gravity and perform experiments with created web sites
• · Determine if the relations between pseudo-gravity (see Epilogue) and gravity would help refine our concepts of how best to facilitate graph navigation.
• · Further develop the theory of graph landmarks and pseudo-gravity and perform experiments to determine if landmarks and vantage points in a graph assist with navigation?

8) Epilogue: Expansion of the theory of gravity and its application to navigation

Consider graphs that have a gravitational landmark (or simply a landmark). These are graphs which may not have a flavoring that motivates perfect navigation between all pairs of nodes but have a flavoring that guides perfect navigation from anywhere to a given designated node (called a landmark). Another class of graphs would have multiple landmarks as shown in the graph below:

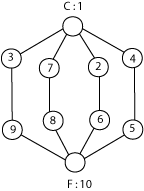
The nodes C and F are landmarks (designated as ceiling and floor, because of their gravity values. The graph is not gravitational, but it does have at least two landmarks. So long as this graph has F labeled 10 and C labeled 1, then so long as all the nodes at level 2 (those connected to node 1) are less than their neighbor at level 2, then the flavoring will route us to the landmarks.

The landmark number of a graph is the maximum number of landmarks for a graph (considered across all possible labelings). In the case that a graph is a gravity graph, its landmark number is N = the number of its nodes.

An allied concept is that of the vantage point. A vantage point is a point from which the given labeling provides a shortest path to any other node. The second graph, below, shows that the floor and ceiling of the above graph can be relabeled so that they are both vantage points (allowing us to get from any point to either F or C, or to get from either F or C  to any specified point via a shortest path). In the earlier labeling, Node 1 did not see the shortest path to 6 (being drawn instead toward its neighbor 7).  The vantage point number of a graph is the maximum number of vantage points that any labeling of that graph allows. Clearly, when the graph is a gravity graph, then each node is both a vantage point and a landmark, and the graph’s landmark number equals its vantage point number.

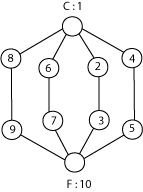
By considering the landmark number and vantage point numbers, of a graph, we have softened the concept of gravitation to what we might call pseudo-gravity: relatively local field effects that might guide navigation in certain subgraphs.

As with multi-dimensional gravity, there are several questions that we have only begun to investigate:

• · Do all graphs have vantage points or landmarks?
• · If a node is a landmark under one flavoring, must it also be a vantage point under another flavoring?
• · What is the relationship between the landmark number and the vantage point number of a graph? If one takes the star (K_1,n), and attaches to each leaf a spindly path of arbitrary length, then it is easy to flavor the graph so that the center of the star is, in fact, a vantage point. However, when this is done, it is almost assuredly not a landmark!

Another generalization is as follows. Consider a graph and a labeling of that graph. Between how many ordered pairs of nodes (p,q) does that labeling motivate the best navigation from p to q? That number is called the flavor count of the labeling.   A labeling of the graph which maximizes (across all labelings)  the flavor count is called a gravitationally maximal flavoring and the flavor count of such a  maximal flavoring is called the flavor count of the graph F(G). In the case of a gravity graph, its flavor count is equal to the number of ordered pairs of nodes:
N(N-1).

That direction of traversal is relevant (and we must consider the order of the pair of nodes can be seen in the first diagram for nodes  4 and 2). From 4 to 2, gravity would lead us (4, 1, 2): a shortest path. From node 2, alas, we would be drawn to node 6, since it appears to be closer to 4 than the other choice, node 1.

Each labeling of a graph (that in essence, gives us the ability to look ahead one node) provides best navigation, in both directions,  between any pair of nodes that share an edge. So for a connected graph having N nodes and L lines, we have that F(G) is at least 2L.  If there is a vantage point or a landmark, then F(G) is likely to be higher since along each of the subpaths leading from the vantage point or to the landmark, the subpath is properly flavored.

7) References

(1): A Browser-based Graphical User Interface for Designing and Manipulating Graphs. David Dailey, Eric Elder, Reno Perri. 7^th Annual Conference, SVGOpen .W3C and SVG Working Group Fall 2009 at Google, Inc.

https://www.svgopen.org/2009/papers/42-Grapher__an_open_source_SVGbased_web_application_for_graph_theorists/

(2) A non-Euclidean Distance. Stanley R. Clemens. The Mathematics Teacher, v. 64, No 7 (November 1971) pp 595-600. Available at http://www.jstor.org/discover/10.2307/27958625?uid=3739864&uid=2129&uid=2&uid=70&uid=4&uid=3739256&sid=21101160785097

(3) http://www.cs.mcgill.ca/~jsatta/pr644/freeman/mmetric.html

(4) Graph Theory by Frank Harary, publ. Addison Wesley, 1970.

(5) Graphs: basic definitions. David Dailey, 2000, http://srufaculty.sru.edu/david.dailey/graphs/graphs.htm

(6) “On the Graphical Containment of Discrete Metric Spaces” David Dailey, Discrete Mathematics, 1994, 131, 51-66.

(7) Distance in Graphs. Buckley and Harary, Addison-Wesley Pub. Co., January 1990.

(8) Training procedures for map learning Thorndike, Perry and Stasz, Cathleen, RAND Corporation. 1979 (http://www.rand.org/pubs/notes/N1018.html)

(9) Navigation in Electronic Worlds, Susanne Jul and George W. Furnas SigCHI 1997, ,

(10) Human spatial navigation: cognitive maps, sexual dimorphism, and neural substrates. Eleanor A Maguire*, Neil Burgess† and John O’Keefehttp://www.icn.ucl.ac.uk/nburgess/papers/maguireburgess99.pdf

(11) Magnetic orientation and magnetoreception in birds and other animals, Wolfgang Wiltschko, Roswitha Wiltschko. J Comp Physiol A (2005) 191: 675orec

(12) Non-Euclidean Geometry, Wikipedia, 2012. http://en.wikipedia.org/wiki/Non-Euclidean_geometry

(13) Floyd, Robert W. (June 1962). “Alogithm 97: Path Matrix”. Communications of the ACM 5(6):345.