Chapter 10:
Balanced Search Trees (2-3-4)
Data Structures and Algorithms in Java
CpSc 374
Binary Search trees work well if random numbers insserted. Don't work as
well if sorted data inserted. Binary search trees can de-generated into a linked list.
Red-Black trees (Chapter 9 which is being skipped), 2-3 trees, and 2-3-4 trees solve this problem of
un-balanced trees.
2-3-4 Trees
- Each node may store 1 to 3 three data items
(key values, with a reference to actual data)
- Items are in sorted order (a < b < c)
- Treat like an ordered array
- Leaf nodes have no children (by definition)
- All leaf nodes are on the same level!
- Each internal node may have 2, 3 or 4 children.
- The number of children is always one more than the number of keys in the node
- No duplicate (equal) keys
- For each internal node,
- All data (k) in the first child precedes the first key (a) in the node;
- k < a
- All data (k) in the second child follows the first key (a), but precedes the second (b)
- a < k < b
- All data (k) in the third child follows the second key, but precedes the third (c)
- b < k < c
- All data (k) in the fourth child follows the third data item.
- k > c
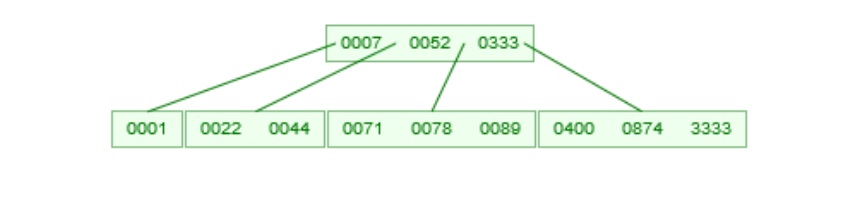
Balanced search trees of Order 4: 2-3-4 trees
Search in 2-3-4 trees
- search algorithm is similar to binary search trees
- In the example 2-3-4 tree, the search for 10 is carried out as follows:
- Compare 10 to the only item in the root. 10 > 4, continue the search in the second child.
- 10 > 6 and 10 > 8, continue the search in the third child.
- 10 > 9, 10 = 10. Stop.
- The efficiency of the search operation is guaranteed to be O(log N)
- For an average of 2 keys per node, the efficiency is proportional to
- 2log4(N)
- On average, it will be better than the search efficiency in 2-3 trees, because the height of a 2-3-4 tree might be less than the height of the 2-3 tree with the same data.
Insertion in 2-3-4 trees
- Step 1 Search for the item to be inserted
- Step 2 Always insert at the leaf level.
- The following cases are possible:
- The termination node is a 2-node (one key)
- make it a 3-node
- insert the new item (16) appropriately
- The termination node is a 3-node (two keys)
- make it a 4-node
- insert the new item (20)appropriately
- The termination node is a 4 node (three keys)
- Split is required
- Split Rule 1:During the search step (while moving down through tree):
- every time a 4-node is encountered, transform it into two 2-nodes
- For root, see Rule 2.
- Create a sibling node.
- Pass right key and two rightmost children to new sibling
- Children maintain relationship to rightmost key
- Pass middle key to parent and link new sibling to parent
- Left and Right child (the new sibling) of promoted key maintains relationship to the promoted key
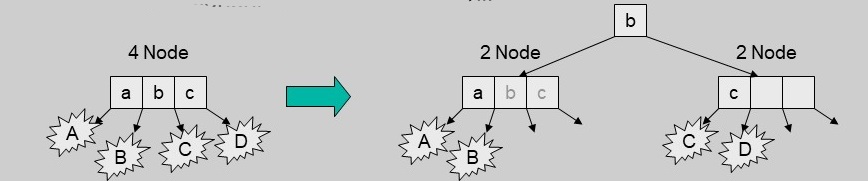
- How do we know there will be room for "b" in the parent?
- Rule 2: If root is a 4-node.
- Create a new root node and a new sibling
- Pass right key and two rightmost children to new sibling
- Children maintain relationship to rightmost key
- Pass middle key to new root and link both the node being split and the new sibling to parent
- Children of promoted key maintain their relationship to the promoted key

- Note that two 2-nodes resulting from these transformations have the same number of children as the original 4-node. This is why the split of a 4-node does not affect any nodes below the level where the split occurs.
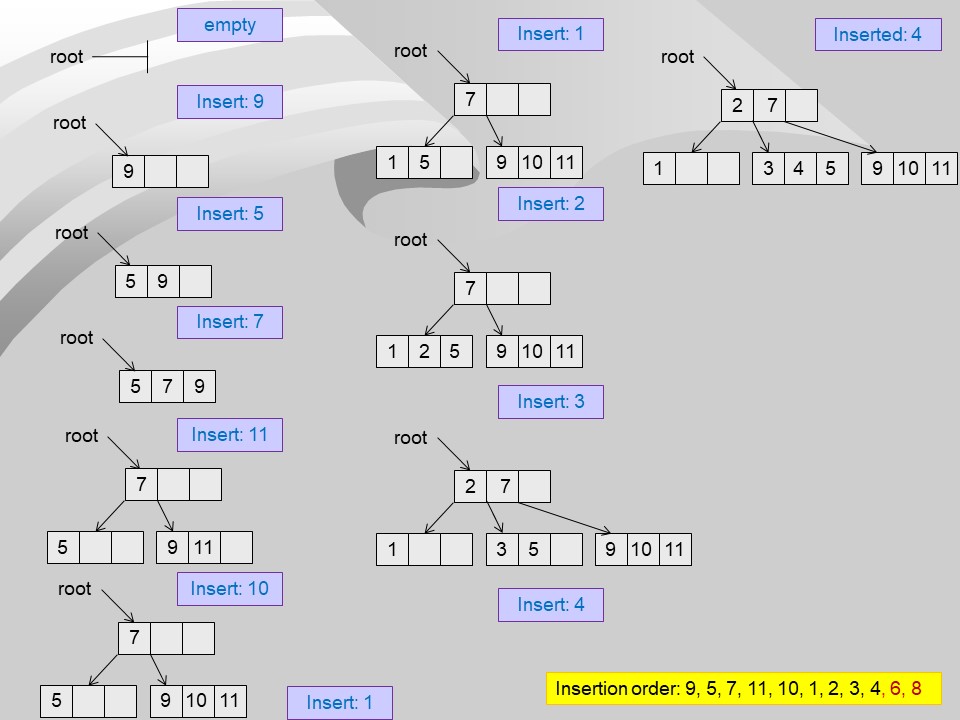
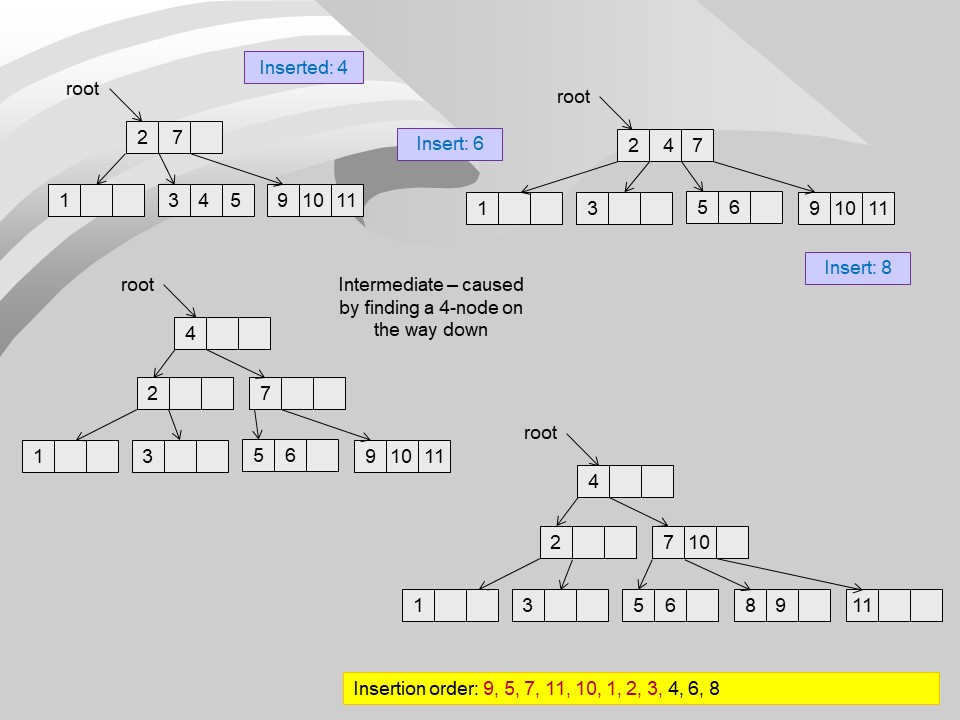
- There will always be room for promotion.
- If there wasn't, it would have been split... making room.
- After insertion, there may be 4-nodes created by insertion.
- They will be split when next encountered during an insertion.
- Splitting the root increases depth of tree by one level
Efficiency of search and insert operations
- Search in a 2-3-4 tree with N nodes takes at most O(log2 N) time
- This is the case if all nodes are 2 nodes.
If there are 3-nodes and 4-nodes on the tree, the search will take less than (log3 N) time.
- Insertion into a 2-3-4 tree takes less than O(log3 N) time
- on average requires less than 1 node split
Deletion in 2-3-4 tree
- Consider our example tree (Insertion order: 1..11)
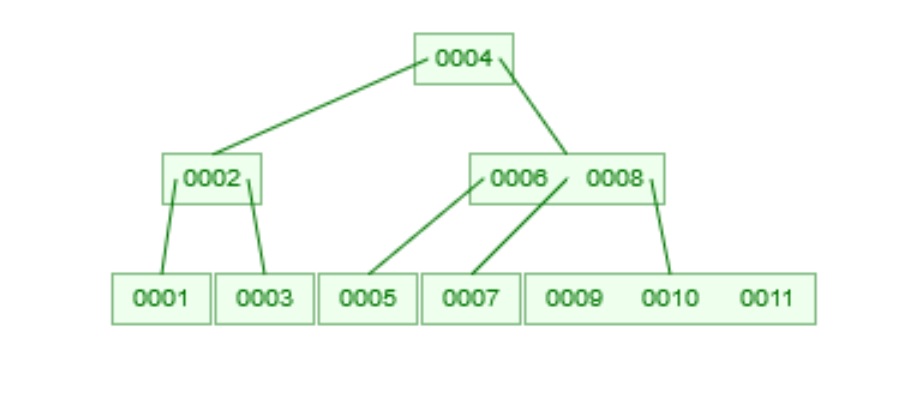
- The following special cases (with multiple sub-cases each) are possible:
- The item is deleted from a leaf node, which currently contains 2 or 3 items.
- delete the item transforming a 4-node into a 3 node
- No other nodes are affected
- Example: delete 9 - the existing 4 node, containing 9, 10, and 11 is transformed into a 3 node, containing 10 and 11.
- delete the item transforming a 3 node into a 2 node
- No other nodes are affected
- delete 11, creating a 2 node with just 10.
- The item is deleted from a leaf node, which currently contains 1 item.
- Delete 7 from the 1..11 tree
- item from the parent node to be drawn down,
which in turn must be replaced by an item from the sibling node.
- (Assuming the sibling node is NOT a 2-node as well.... See case 2.

- Case 2 (with several more sub-cases)
- Delete from a node that has non-external children.
- delete 7 (from image below)
- This case can be reduced to case 1
- find item that precedes the one to be deleted in in-order traversal (i.e., 6)
- exchange the two items
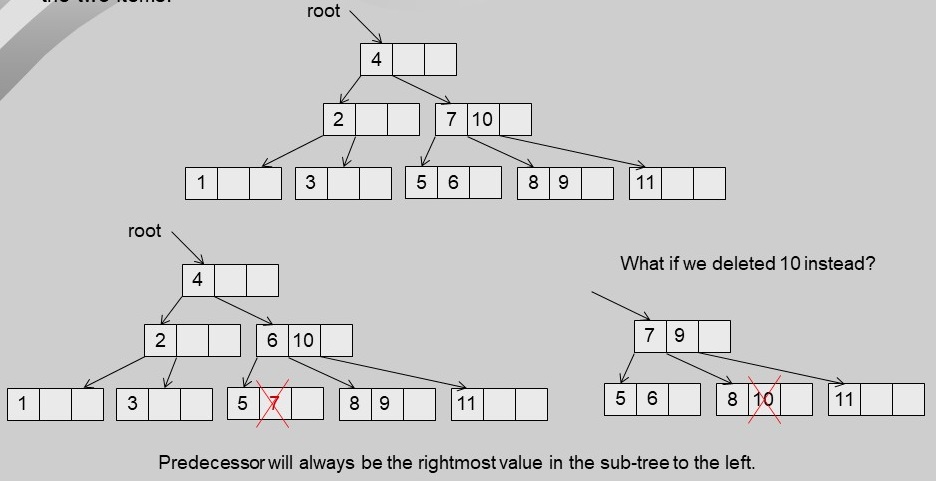
- Delete from a node that has non-external children.
- delete 8 from the original tree
- This case can be reduced to case 1
- find item that precedes the one to be deleted in in-order traversal (i.e.,7)
- exchange the two items.
- However, 8 is now the only item in the node;
we have a case of underflow
- transfer an item from the parent node to the underflow node
- substitute a successor from the sibling node (9 is the successor of 7).
- In our example, 7 will be transferred back to where it was
- and 9 will move to the parent node to fill the gap.
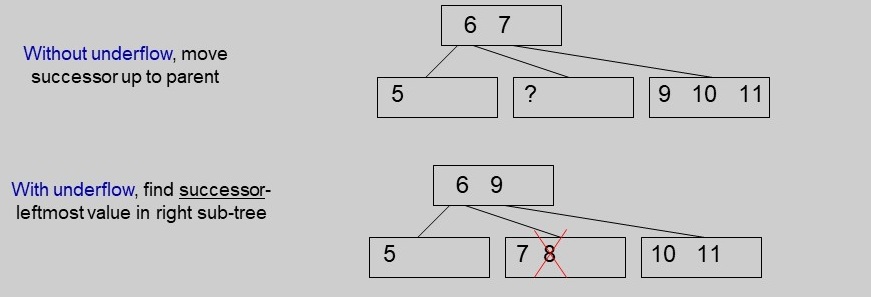
- if the sibling node is also a 2-node, fusing takes place (Delete 6 in
image below. exchange 5 and 6. only 1 item, put 5 back.)
- the two 2-node siblings are "fused" in a single 3-node
- after an item is transferred from the parent node
- the parent can now handle one less child, and has one child less after two of its former children are fused.
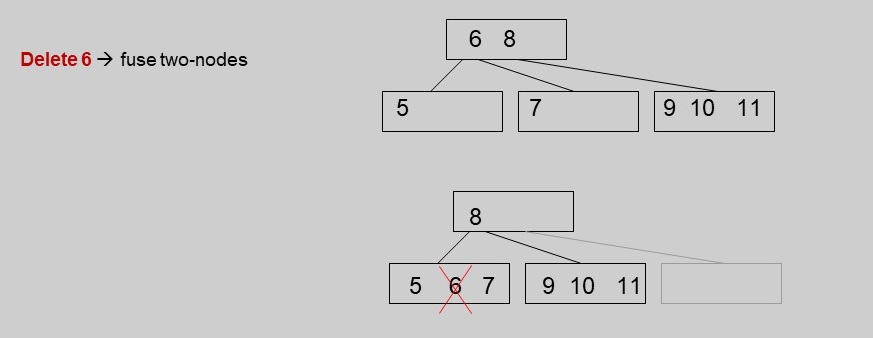
- Can borrow all the way up to root
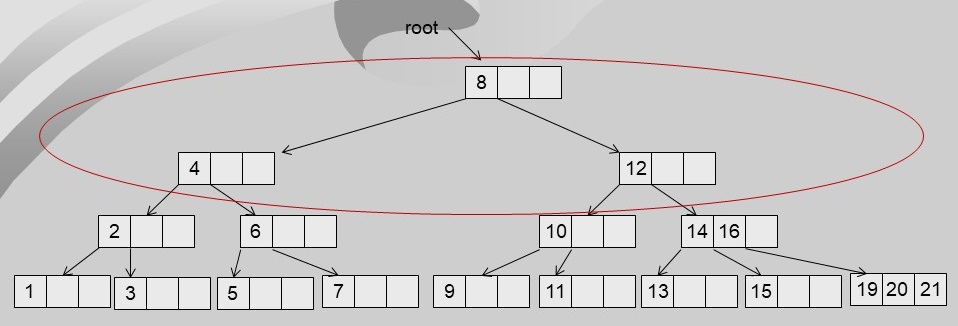
- Example: Delete 1
- 1 is in a leaf, but it is a 2-node --> borrow from sibling
- But sibling is also a 2-node --> borrow from parent
- But parent is also a 2-node... all the way up to the root
- We know that all of these are 2-nodes --> fuse these three
- Tree loses a level!

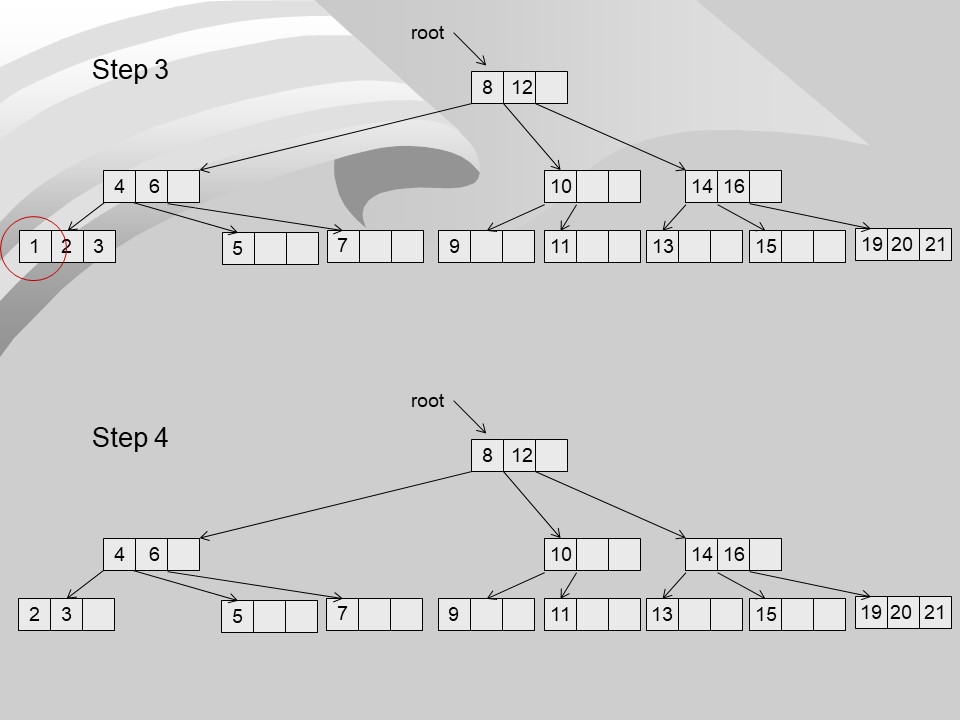
- Visualization
- Practice
2-3 Trees
- Similar to 2-3-4 trees
- But each node has 1 or 2 keys
- and each node has 2 or 3 children
- All leaves still at same level and have no children
2-3 Tree Insertion
- No splits occur during search
- Insertion is always in a leaf
- If leaf has room, insert in order
- If leaf has two keys (full), a split must occur...
- New key must particpate in split, as we need three values
- Ripple Effect of Split
- Create new node
- Largest key moves to new node
- Middle key is promoted to parent
- Repeat insertion.
- This may cause parent to split.
- Splitting may ripple up (recursively) to the root
- If root is split, tree depth grows by one level
B-Trees & External Storage
- Disk access is slow & is done by reading blocks of data
- Accesses for searching, inserting & deleting should be based on block size
- Records should consider block size
- The index should also acknowledge block size
- Note - often use a multiple of block size
Disks are Slow (except SSD)
- Total access time = seek + settle + command + latency
- 2.8 ms ... 28.4 ms
- Seek time - head actuator moves to proper track (8-9 ms)
- Settle time - time for heads to stabilize (~0.1 ms)
- Command overhead - time for disk to react to a command (~0.5 ms)
- Latency - waiting for sector to rotate under head
- 3600 rpm -> 8.3 ms (avg)
- 15,000 rpm -> 2.0 ms (avg)
- Tranfer rate - the rate at which data can be read/written from/to disk
- Includes internal & external transfer, media & sustained rates
- 100 MBps -> 8*108 bps -> 1.2 ns/bit -> 0.08 ms/8K block
- By comparison, access rates (latency) for memory are 10-20 ns
- Hence, author's "10,000 time faster" is conservative.
Trees of Order m = k+1
- A 2-3 tree is a multiway tree of order 3
- A 2-3-4 tree is a multiway tree of order 4
- Want a node to be the "same" size as a block (B), to speed access
- Our pointers (or references) are block numbers on a disk - assume ints and 4 bytes each
- If record size is S,
- kideal = floor((B-4) / (S+4))
- wasted space = B --k(S+4) - 4 bytes
- m = k + 1
- Example, m=17
- Block size is 8K, or 8,192 bytes
- Record size is 507 bytes
- k = floor( (8192 - 4) / (507 + 4) )
- = 16 records per block
- One block (or node) can hold 16 records & have 17 refs (children)
- B-Tree of order 17
- Wasted space in each block: 12 bytes
Properties of B-Tree
- Maintains search tree relationship between parent keys and child sub-trees
- All leaves are at same level
- All nodes have at least ceil(m/2)-1 keys
- Two half-full nodes can be merged into a legal node
- All internal nodes have at least ceil(m/2) non-empty children
- Except the root, which may have 0, 2, or more
- A full node can be split into two legal nodes
Efficiency Issues
- Want each node to hold lots of data
- ceil(m/2)-1 .. (m-1) keys
- If all nodes filled: logm N levels or accesses
- All nodes ~half filled: h = logceil(m/2) N
- More precisely, using our example of m=17...
- h <= log9 (n+1)/2
- Searching is fast (compared to sequential or binary search on disk)
- See text for (contrived) comparison example
- To keep nodes more full, we use 2-3 insertion strategy
- Do not split nodes while traversing tree looking for insertion location
- Splits occur at leaves and ripple up
Insertion
- Search for location in leaf
- Easy case, simply add it to leaf node (in order)
- Full leaf => split (recursive)
- Create new node(s)
- In RAM, insert new key in order (merge)
- Median key is promoted
- Lower half of keys stay
- Right half of keys go to new node
- Indexing: Speeding Up Access
- Want higher order B-Tree...
- Instead of keeping record in Node, only keep the key value
- Record size is 507 bytes
- But, key size is only 28 bytes
- k = floor((8192-4)/(28+4)) = 255
- B-Tree of order 256
- log9 500,000 = 6.0
- log128 500,000 = 2.7 --> 4 disk accesses












